УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА

Из закона Авогадро следует, что массы равных объемов двух газов относятся друг к другу, как их молярные массы:

D = = 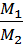. (2.2)

Величиной D называется относительная плотность первого газа по второму.

ПРИМЕР: плотность кислорода по воздуху D = 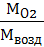= = 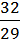1,1.

Объединенное уравнение, описывающее состояние идеального газа, носит название УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА (уравнение Клапейрона – Менделеева):

PV= nRT, (2.3)

где для газов n = 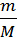= 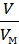. В этом уравнении Р(Па) - давление, при котором

находится данное количество газа; V(м³) - объем, занимаемый газом; n (моль) – число молей газа; Т (К) – абсолютная температура; R (8,31 Дж/моль·К) –

универсальная газовая постоянная (R – это работа расширения 1 моль идеального газа при нагревании его на 1 градус). Универсальная газовая постоянная связана с константой Больцмана соотношением

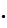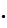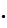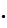R=k N_a = 13,805 10 ^-22 6,02 10²³ = 8,31 Дж/моль·К.

Для расчета параметров газа, находящегося в смеси с другими газами, используют понятие парциального давления.

Парциальное давление газа– это давление, которое оказывал бы данный газ, если бы занимал весь объем, занимаемый газовой смесью. Общее давление газовой смеси равно сумме парциальных давлений отдельных газов. Парциальные давления газов в смеси пропорциональны их объемному содержанию.

ПРИМЕР: газовая смесь (воздух) состоит на 20% из кислорода и на 80% из азота. Давление воздуха составляет 1 атмосферу. В этом случае парциальное давление кислорода Р_О2 = 0,2 атм., а парциальное давление азота – Р_N2=0,8 атм.

СТРОЕНИЕ АТОМА

Простейшая модель строения атома в современной науке принадлежит Резерфорду. Согласно этой модели атом представляет собой электронейтральную систему, состоящую из положительно заряженного ядра и совокупности отрицательно заряженных электронов, которые двигаются в поле этого ядра. Заряд ядра и порядковый номер элемента в таблице Д.И.Менделеева определяется числом протонов в ядре. Формальный заряд протона равен +1. Число электронов в атоме равно числу протонов в его ядре. Формальный заряд электрона -1. Модель Резерфорда не могла объяснить природу устойчивости атомов (согласно классической механике заряженная частица – электрон, двигаясь по круговой или иной орбите вокруг ядра, должна непрерывно испускать энергию и в течение 10^-6с упасть на это ядро. Этого не происходит. Время жизни отдельных атомов может

превышать миллиарды лет. Кроме того, была не понятна зависимость химических свойств атомов от заряда их ядра и способность испускать и поглощать энергию в виде строго определенных порций – квантов. В 1913 году датский физик Нильс Бор попытался объединить модель Резерфорда с квантовой теорией Макса Планка. Созданная им теория строения атома водорода базируется на двух постулатах: 1.В атоме существуют некоторые орбиты, по которым электрон может двигаться не испуская и не поглощая энергии;

2.При переходе электрона с одной орбиты на друную атом испускает или поглощает энергию строго определенной частоты.

В рамках своей теории Бор получил уравнение полной энергии электрона в атоме, а также уравнения, позволяющие рассчитать скорость электрона и радиус разрешенных орбит. Оказалось, что полная энергия электрона в атоме - величина отрицательная. Электрон может находиться в составе атома до тех пор, пока его положительная кинетическая энергия будет меньше по абсолютной величине, чем его отрицательная потенциальная энергия взаимодействия с ядром.

Уравнения представляют собой набор постоянных величин (констант), кроме множителя n, котрый может принимать значения любых целых чисел − 1,2,3,4 …. Значение множителя n соответствует номеру разрешенного электронного уровня, по которому электрон может двигаться без изменения своей энергии. При переходе с уровня на уровень энергия электрона меняется скачкообразно, так как между ними электрон существовать не может. Повышение номера уровня соответствует увеличению энергии электрона, а понижение – уменьшению энергии. Таким образом, наименьшим запасом энергии электрон обладает находясь на первом энергетическом уровне (первой боровской орбите). Это положение соответствует минимальному запасу энергии атома и, значит, наиболее устойчивому состоянию. Переход электрона на вышестоящие уровни определяется термином «возбужденное состояние атома». Возврат атома в нормальное состояние соответствует переходу электрона на исходный энергетический уровень, при этом атом последовательно испускает кванты (порции) энергии, соответствующие разнице энергий между разрешенными уровнями.

Эти кванты энергии фиксируются специальными приборами, в результате чего исследователи получают атомный спектр, который имеет вид набора светлых и темных полос, лежащих в определенной области спектра.Чем ближе к ядру атома располагается разрешенный электронный уровень, тем больше энергия (короче длина волны), необходимая для возбуждения атома.

Дальнейшее развитие учения о строении атома связано со становлением науки, получившей название квантовая механика. В основе ее лежат корпускулярно- – волновые представления о природе микрочастиц.

Луи де Бройль в 1924 году вывел соотношение, которое получило его имя :

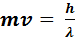, (3.1)

где m – масса частицы; ν – скорость частицы; h – постоянная Планка; λ – длина волны. Согласно этому соотношению любой частице, обладающей массой m и движущейся со скоростью , соответствует длина волны λ.

В 1927 году немецкий физик В.Гейзенберг вывел положение, получившее название «принцип неопределенности Гейзенберга», согласно которому невозможно одновременно точно определить координаты микрочастицы и ее скорость (импульс). Чем точнее определяется местоположение частицы, тем менее точно можно определить ее скорость. Эта неопределенность заставила отказаться от понятия траектория движения электрона. Было введено понятие вероятности нахождения электрона в различных точках атомного пространства, а вместо боровских разрешенных орбит понятие «электронная орбиталь».

Последний термин обозначает часть околоядерного пространства, где электрон бывает с максимальной долей вероятности. Область этого пространства, в которой электрон проводит более 90% своего времени называется граничная поверхность.

В 1926 году австрийский физик Э.Шредингер предложил уравнение, связывающее воедино корпускулярно-волновые свойства микрочастиц с их

энергией. В уравнение входит величина ψ, называемая волновой функцией. По существу, волновая функция – это решение уравнения Шредингера, называемое «атомная орбиталь». Квадрат этой функции ψ² – определяется как вероятность нахождения электрона в разных точках атомного пространства.

Расчеты, сделанные для атома водорода показали, что точки атомного пространства, где электрон находится с максимальной долей вероятности, образуют пространственную фигуру, практически полностью по форме и размерам совпадающую с первой боровской орбитой.

Изучение атомных спектров многоэлектронных атомов показало, что они имеют более тонкую структуру, чем простые линии. Внутри линий были обнаружены пакеты более тонких линий – «мультиплетов», появление которых связано с взаимодействием электрона со своими соседями. Эти взаимодействия были учтены, когда для описания движения электронов в теории Бора были использованы четыре квановых числа.

КВАНТОВЫЕ ЧИСЛА

Состояние каждого электрона в атоме обычно описывают с помощью четырех квантовых чисел: главного (n), орбитального (l), магнитного (m) и спинового (s). Первые три характеризуют движение электрона в пространстве, а четвертое - вокруг собственной оси.

Главное квантовое число (n) определяет полную энергию электрона на энергетичеком уровне и, следовательно, номер энергетического уровня электрона,

удаленность уровня от ядра, размер электронного облака, принимает целые значения (n = 1, 2, 3 ...) и соответствует номеру периода. Из периодической системы для любого элемента по номеру периода можно определить число энергетических уровней атома, а также какой энергетический уровень является внешним.

Например, элемент кадмий Cd расположен в пятом периоде, значит n = 5. В его атоме электроны раcпределены по пяти энергетическим уровням (n = 1, n = 2, n = 3, n = 4, n = 5); внешним будет пятый уровень (n = 5).

Орбитальное квантовое число ( l ) характеризует момент количества движения электрона (mvr), а значит, и геометрическую форму орбитали, принимает значение целых чисел от 0 до (n - 1). Независимо от номера энергетического уровня, каждому значению орбитального квантового числа соответствует свое буквенное обозначение и орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем c одинаковыми n и l - подуровнями.

l=0 s- подуровень, s- орбиталь – орбиталь сфера

l=1 p- подуровень, p- орбиталь – орбиталь гантель

l=2 d- подуровень, d- орбиталь – орбиталь сложной формы

l=3 f-подуровень, f-орбиталь – орбиталь еще более сложной формы

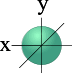
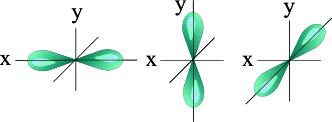
S – орбиталь. Р - орбитали: Р_х Р_у P_z

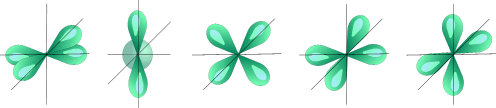
d- Орбитали: d_x²_-y² d_z² d_xy d_yz d_xz

орбитали

На первом энергетическом уровне (n = 1) орбитальное квантовое число принимает единственное значение l = (n - 1) = 0. Форма обитали - сферическая; на первом уровне только один подуровень - 1s. Для второго энергетического уровня (n = 2) орбитальное квантовое число может принимать два значения: l = 0, s- орбиталь - сфера большего размера, чем на первом энергетическом уровне; l = 1, p- орбиталь - гантель. Таким образом, на втором энергетическом уровне имеются два подуровня - 2s и 2p. Для третьего энергетического уровня (n = 3) орбитальное квантовое число l принимает три значения: l = 0, s- орбиталь - сфера большего размера, чем на втором энергетическом уровне; l = 1, p- орбиталь - гантель большего размера, чем на втором энергетическом уровне; l = 2, d– орбиталь сложной формы.

Таким образом, на третьем энергетическом уровне могут быть три энергетических подуровня – 3s, 3p и 3d.

Магнитное квантовое число (m) характеризует изменение энергии орбиталей одного подуровня во внешнем магнитном поле. Это обусловлено различным направлением орбиталей в пространстве. Можно сказать, что m характеризует положение электронной орбитали в пространстве и принимает целочисленные значения от -l до +l, включая 0. Это означает, что для каждой формы орбитали существует (2l + 1) энергетически равноценных ориентации в пространстве.

Для s- орбитали (l = 0) такое положение одно и соответствует m = 0. Сфера не может иметь разные ориентации в пространстве.

Для p- орбитали (l = 1) - три равноценные ориентации в пространстве (2l + 1 = 3): m = -1 (Р_у)_,, 0 (P_z), +1 (Р_х, ).

Для d- орбитали (l = 2) - пять равноценных ориентаций в пространстве (2l + 1 = 5): m = -2 (d_xy ), -1 (d_yz ), 0 (d_z² ), +1 (d_xz ), +2 (d_x²_-y² ).

Таким образом, на s- подуровне - одна, на p- подуровне - три, на d- подуровне - пять, на f- подуровне – 7 орбиталей.

Спиновое квантовое число (s) характеризует магнитный момент, возникающий при вращении электрона вокруг своей оси. Принимает только два значения: +1/2 и –1/2, соответствующие противоположным направлениям вращения.