Корреляция между качественными и количественными признаками, а также между двумя качественными признаками

Предложено много разных методов и показателей, в том числе:

1) Коэффициент ассоциации или тетрахорический показатель связи (качественные признаки, группируемые в четырехпольную корреляционную таблицу).

Пример – оценка сцепления генов

2) Коэффициент взаимной сопряженности или полихорический показатель связи (Пирсона-Чупрова) (качественные признаки, группируемые в многопольную корреляционную таблицу).

Имеется и возможность оценить корреляционную связь между качественным и количественным признаками.

Частная и множественная корреляция

Частная корреляция

Зная парные коэффициенты корреляции r_xy, r_xzи r_yz, можно определить т.н. частные или парциальные коэффициенты корреляции, показывающие корреляционную зависимость между двумя варьирующими признаками при постоянной величине третьего признака (т.е. при исключенном влиянии третьего признака).

Для определения частного коэффициента корреляции между признаками Х и Y при постоянной величине признака Z применяют формулу:

.

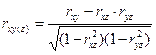Заключение знака в скобки означает, что влияние признака Z на корреляцию между Х и Y исключено.

Аналогичные формулы получены для r_xy(z)и r_yz(x).

Пример.

В предыдущей лекции отмечалось, что установлены следующие коэффициенты парной корреляции:

1) урожайность (Y) – температура в июне (Х) r_xy=-0.38;

2) урожайность (Y) – сумма осадков за июнь (Z) r_yz=0.37;

3) температура в июне (Х) – сумма осадков за июнь (Z) r_xz=-0.43.

Тогда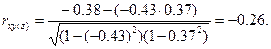

Сравнение частного коэффициента корреляции 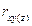=-0.26 с парным r_xy=-0.38 позволяет утверждать, что при одинаковом уровне осадков в июне связь урожайность – температура июня меньше, чем при изменчивом.

Частные корреляции используются редко.

Анализ множественных нелинейных связей сложен, он описан в специальной литературе.