Внутренняя энергия идеального газа
Молекулы газа, совершая хаотическое движение, в соударениях изменяют свою скорость, поэтому в газе есть молекулы с различными скоростями в интервале от 0 до 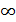 (но следует иметь в виду, что даже большие скорости молекул
(но следует иметь в виду, что даже большие скорости молекул 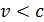 , равной
, равной 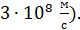 Соответственно, и кинетические энергии молекул газа различны. Поэтому вводят средние характеристики молекул. Согласно закону Больцмана о равномерном распределении энергии молекул по степеням свободы, средняя энергия молекулы
Соответственно, и кинетические энергии молекул газа различны. Поэтому вводят средние характеристики молекул. Согласно закону Больцмана о равномерном распределении энергии молекул по степеням свободы, средняя энергия молекулы 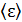 зависит от температуры газа T следующим образом:
зависит от температуры газа T следующим образом:
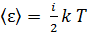 , (5)
, (5)
где i – суммарное число степеней свободы молекулы газа:
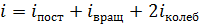 .
.
Для молекул при невысоких температурах ( 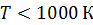 ) величина
) величина 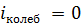 . Число степеней свободы молекулы связано с числом атомов в молекуле и ее структурой (см. таблицу).
. Число степеней свободы молекулы связано с числом атомов в молекуле и ее структурой (см. таблицу).
Таблица
| Газ | Одноатомный (He, Ne, Arи др.) | Двухатомный
( 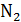 , , 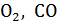 и др.) и др.)
| Трех- и многоатомный
( 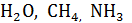 и др.) и др.)
|
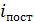
| |||
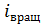
| – | ||
| i |
Внутренняя энергия идеального газа U – это функция состояния газа, равная сумме кинетических энергий всех молекул, так как для невзаимодействующих молекул идеального газа 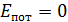 . Таким образом, величина внутренней энергии
. Таким образом, величина внутренней энергии
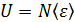 ;
;
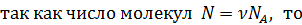 внутренняя энергия идеального газа
внутренняя энергия идеального газа
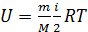 , (6)
, (6)
где m и M – масса газа и молярная масса; R – молярная газовая постоянная.
4.1.3. Распределение молекул идеального газа по скоростям –
Закон Максвелла
Закон Максвелла описывается функцией 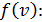
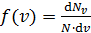 .
.
Здесь 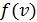 – функция распределения молекул по скоростям; она равна доле молекул, имеющих скорости в единичном интервале
– функция распределения молекул по скоростям; она равна доле молекул, имеющих скорости в единичном интервале 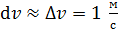 вблизи данной скорости
вблизи данной скорости 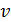 . Закон распределения молекул идеального газа по скоростям имеет следующий вид:
. Закон распределения молекул идеального газа по скоростям имеет следующий вид:
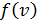
|
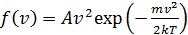 , (7)
, (7)
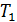
|
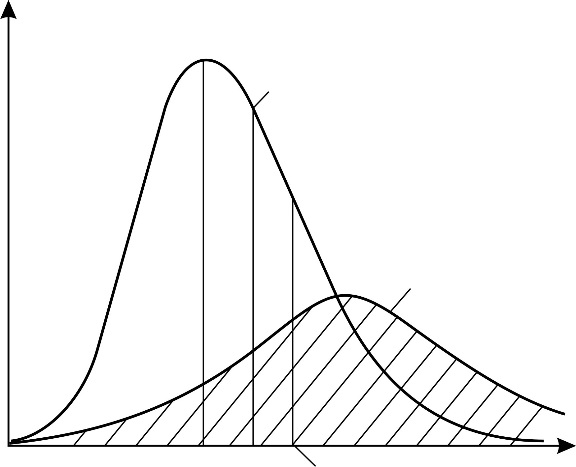
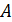 – постоянная, не зависящая от скорости; m – масса молекулы. На графике (рис. 16) функция (7) имеет вид кривой с максимумом.
– постоянная, не зависящая от скорости; m – масса молекулы. На графике (рис. 16) функция (7) имеет вид кривой с максимумом.
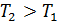
|
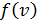
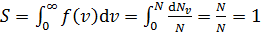 ,
,
| Рис. 16 |
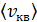
|
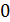
|
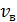
|
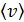
|
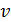
|
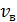 – наиболее вероятная скорость молекулы, она соответствует максимуму кривой распределения. Из условия максимума функции
– наиболее вероятная скорость молекулы, она соответствует максимуму кривой распределения. Из условия максимума функции 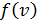 получена величина
получена величина
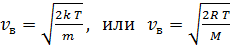 , (8)
, (8)
Средняя квадратичная скорость молекулы определяется по величине средней кинетической энергии поступательного движения молекулы (см. формулу (5)):
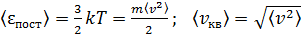 ;
; 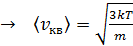 . (9)
. (9)
Средняя скорость молекулы 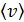 (средняя арифметическая скорость) определяется с помощью закона статистического распределения
(средняя арифметическая скорость) определяется с помощью закона статистического распределения 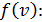
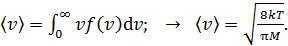 (10)
(10)
Сравнивая средние значения скоростей молекулы с учетом формул (8), (9) и (10), получаем соотношения, справедливые для молекул идеального газа и удобные в расчетах:
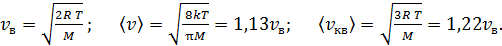 (11)
(11)
Дата добавления: 2016-10-07; просмотров: 2718;











