Механические колебания
Задача 16. Пружинный маятник жесткостью 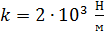 совершает гармонические колебания. Масса груза
совершает гармонические колебания. Масса груза 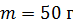 , максимальная скорость груза
, максимальная скорость груза 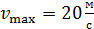 . Определите циклическую частоту
. Определите циклическую частоту 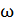 , период
, период 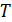 и амплитуду колебаний
и амплитуду колебаний 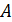 .
.
Дано Решение
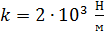 ; ;
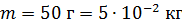 ; ;
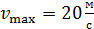 . .
| |
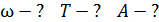
|
Циклическая частота 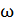 колебаний пружинного маятника определяется формулой
колебаний пружинного маятника определяется формулой
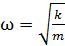 , (1)
, (1)
где k – жесткость пружины; m – масса груза.
Вычисляем частоту 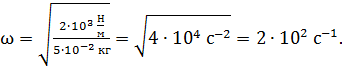
Период колебаний связан с циклической частотой формулой 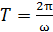 .
.
Вычисляем период колебаний 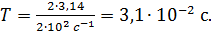
Амплитуду колебаний определим, рассчитывая полную механическую энергию груза, совершающего колебания:
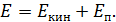 (2)
(2)
При колебаниях груза по закону 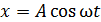 происходит превращение кинетической энергии в потенциальную, причем, в крайних положениях груза, когда смещение
происходит превращение кинетической энергии в потенциальную, причем, в крайних положениях груза, когда смещение 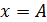 , скорость груза
, скорость груза 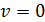 и величина
и величина 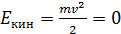 . Следовательно, согласно равенству (2), полная механическая энергия груза
. Следовательно, согласно равенству (2), полная механическая энергия груза
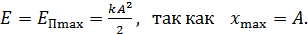 (3)
(3)
При движении груза из крайнего положения потенциальная энергия переходит в кинетическую энергию и в положении равновесия смещение 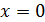 и потенциальная энергия
и потенциальная энергия 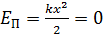 . При этом полная механическая энергия равна максимальной кинетической энергии груза:
. При этом полная механическая энергия равна максимальной кинетической энергии груза:
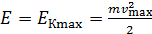 . (4)
. (4)
Приравняем значения полной механической энергии груза, определяемой формулами (3) и (4):
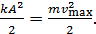 (5)
(5)
Из соотношения (5) выразим определяемую амплитуду колебаний груза
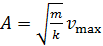 ; с учетом формулы (1) получаем
; с учетом формулы (1) получаем 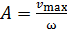 .
.
Вычисляем: 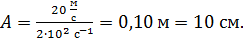
Задача 17. Частица массой 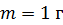 совершает гармонические колебания по закону
совершает гармонические колебания по закону 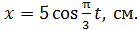 Определите период колебаний
Определите период колебаний 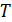 , максимальную скорость частицы
, максимальную скорость частицы 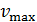 и ее механическую энергию
и ее механическую энергию 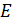 .
.
Дано Решение
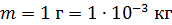 ; ;
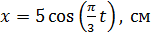 . .
| |
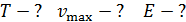
|
Запишем закон гармонических колебаний частицы в виде:
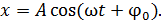 (1)
(1)
Сравнивая с заданным уравнением движения
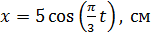 , (2)
, (2)
видим, что циклическая частота колебаний 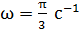 . Период колебаний связан с циклической частотой формулой
. Период колебаний связан с циклической частотой формулой
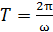 .
.
Подставляя в эту формулу найденное значение частоты, вычисляем:
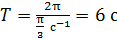 .
.
Скорость движения частицы определяем как первую производную от смещения 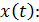
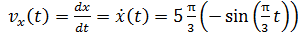 .
.
Получили гармонический закон колебаний величины скорости в виде
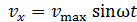 ,
,
где амплитуда скорости частицы 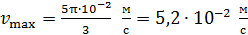 .
.
Полная механическая энергия E частицы, совершающей гармонические колебания (см. решение задачи 16) выражается формулой:
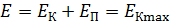 , или
, или 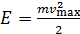 .
.
Вычисляем величину механической энергии колеблющейся частицы:
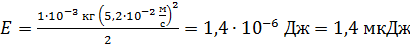 .
.
Задача 18. Материальная точка (МТ) массой m 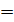 10 г совершает гармонические колебания по закону
10 г совершает гармонические колебания по закону 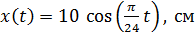 . Определите амплитуду
. Определите амплитуду 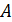 колебаний МТ, модуль ее скорости
колебаний МТ, модуль ее скорости 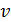 и силу
и силу 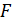 , действующую на МТ в момент времени
, действующую на МТ в момент времени 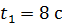 .
.
Дано Решение
m 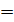 10 г 10 г 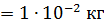 ; ;
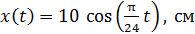 ; ;
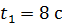 . .
| |
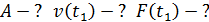
|
Запишем закон гармонических колебаний МТ в виде
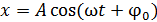 (1)
(1)
и сравним с заданным законом движения:
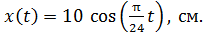 (2)
(2)
Из сопоставления уравнений (1) и (2) видим, что амплитуда колебаний 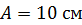 .
.
Скорость МТ найдем как первую производную от зависимости координаты от времени 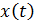 , представленной уравнением (2):
, представленной уравнением (2):
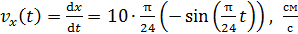 . (3)
. (3)
Вычислим по уравнению (3) значение скорости в момент времени 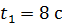 :
:
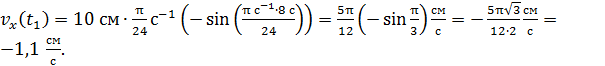
Знак «минус» – отрицательная проекция скорости на ось x, означает, что вектор скорости 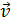 колеблющейся материальной точки в момент времени
колеблющейся материальной точки в момент времени 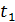 направлен противоположно оси
направлен противоположно оси 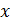 .
.
Силу, действующую на МТ, найдем по закону динамики движения – по второму закону Ньютона:
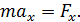 (4)
(4)
Для определения ускорения материальной точки (точнее, его проекции на ось x) используем определительную формулу:
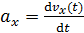 ,
,
где зависимость 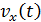 представлена уравнением (3); дифференцируя его, получаем проекцию ускорения на ось
представлена уравнением (3); дифференцируя его, получаем проекцию ускорения на ось 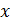 , как функцию времени:
, как функцию времени:
 ,
, 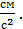 (5)
(5)
Подставляя выражение (5) в формулу закона динамики (4), находим закон изменения силы при гармонических колебаниях МТ в виде:
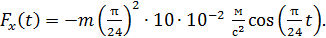 (6)
(6)
С учетом закона колебаний (2) уравнение (6) запишем в следующем виде:
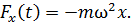 (7)
(7)
Уравнения (6) и (7) показывают, что упругая (или подобная ей сила) изменяется с течением времени по гармоническому закону, как и величина смещения МТ от положения равновесия.
Вычисляем величину проекции силы, действующей на колеблющуюся МТ в момент времени 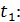
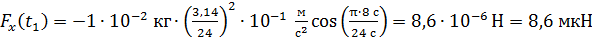 .
.
ЧАСТЬ 2
Дата добавления: 2016-10-07; просмотров: 2460;











