Механические колебания

Гармонические колебания описывают уравнением:

,

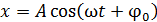где x – смещение колеблющейся точки относительно положения равновесия в момент времени t; 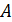– наибольшее смещение, или амплитуда колебаний; w – циклическая частота колебаний; j₀ – начальная фаза колебаний; 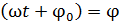– фаза колебаний в момент времени t.

Колебания характеризуют частотой w и периодом T, связанными друг с другом соотношением: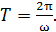

Период колебаний математического маятника

,

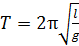где 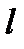– длина маятника; 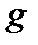– ускорение свободного падения.

Период колебаний пружинного маятника

,

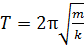где m – масса груза; k – жесткость пружины.

Кинетическая энергия гармонических колебаний

,

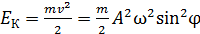где m – масса колеблющегося объекта; 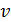– его скорость.

Потенциальная энергия гармонических колебаний

,

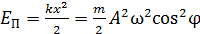где 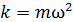– жесткость, или коэффициент упругости пружины.

Результатом сложения одинаково направленных гармонических колебаний равной частоты является также гармоническое колебание с периодом, равным периоду складываемых колебаний. Если уравнения двух складываемых колебаний:

,

,

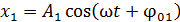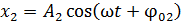то уравнение результирующего колебания:

.

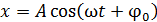Здесь амплитуда результирующего колебания

,

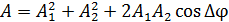где 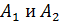– амплитуды складываемых колебаний; 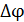– их разность фаз.

Уравнение затухающего колебательного движения имеет вид

.

Здесь 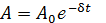является амплитудой затухающих колебаний; 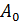–начальная амплитуда (в момент времени 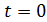); d – коэффициент затухания, его величина 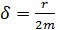, где r – коэффициент сопротивления среды; m – масса колеблющейся точки. Затухание колебаний характеризуют логарифмическим декрементом затухания

,

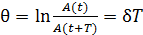где 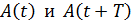– амплитуды двух последовательных колебаний, отделенных друг от друга периодом колебаний T.

Циклическая частота затухающих колебаний

,

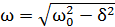где 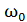– циклическая частота свободных (собственных) незатухающих колебаний той же колебательной системы.