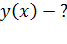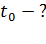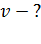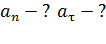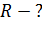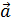Кинематика поступательного и вращательного движения. План решения кинематических задач
1. Сделайте рисунок, на котором покажите оси x и y и вектор начальной скорости 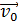 ; этот вектор направлен по касательной к траектории. В случае, если тело после броска совершает движение в поле тяжести Земли под действием силы
; этот вектор направлен по касательной к траектории. В случае, если тело после броска совершает движение в поле тяжести Земли под действием силы 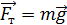 , траекторией движения является парабола или ветвь параболы, а полное ускорение тела равно ускорению свободного падения
, траекторией движения является парабола или ветвь параболы, а полное ускорение тела равно ускорению свободного падения 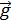 .
.
2. Выясните характер независимых движений вдоль осей x и y: равномерное или равнопеременное. Запишите для этих движений уравнения кинематики в проекции на оси x и y: 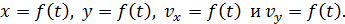
3. Для криволинейного движения используйте также естественные оси – касательную и нормаль к траектории. Такие оси следует показать на рисунке в той точке, где необходимо определить нормальное 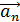 и тангенциальное
и тангенциальное 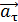 ускорение. Эти ускорения являются составляющими полного ускорения, равного
ускорение. Эти ускорения являются составляющими полного ускорения, равного 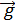 , поэтому для нахождения составляющих необходимо с конца вектора
, поэтому для нахождения составляющих необходимо с конца вектора 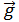 опустить перпендикуляры на нормаль и касательную. Из полученного так треугольника ускорений с помощью функций
опустить перпендикуляры на нормаль и касательную. Из полученного так треугольника ускорений с помощью функций 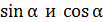 находят величины
находят величины 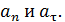 Необходимые значения тригонометрических функций определяют из треугольника скоростей; для его построения в той же точке траектории на рисунке показывают составляющие вектора скорости
Необходимые значения тригонометрических функций определяют из треугольника скоростей; для его построения в той же точке траектории на рисунке показывают составляющие вектора скорости 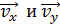 , при сложении которых получается вектор скорости
, при сложении которых получается вектор скорости 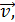 направленный по касательной к траектории.
направленный по касательной к траектории.
4. Если в задаче задан кинематический закон поступательного или вращательного движения, то для нахождения скорости и ускорений используют определительные формулы, последовательно дифференцируя функцию закона движения 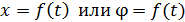 , а затем дифференцируя полученный закон изменения скорости
, а затем дифференцируя полученный закон изменения скорости 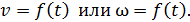
Задача 1. Небольшое тело бросили под углом 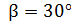 к горизонту с начальной скоростью
к горизонту с начальной скоростью 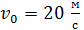 . Пренебрегая сопротивлением воздуха, найдите: 1) уравнение траектории движения тела
. Пренебрегая сопротивлением воздуха, найдите: 1) уравнение траектории движения тела 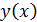 , 2) время движения
, 2) время движения 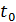 , 3) скорость, нормальное
, 3) скорость, нормальное 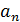 и тангенциальное
и тангенциальное 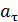 ускорение тела через
ускорение тела через 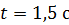 после начала движения, 4) радиус кривизны траектории
после начала движения, 4) радиус кривизны траектории 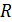 в этот момент времени.
в этот момент времени.
|
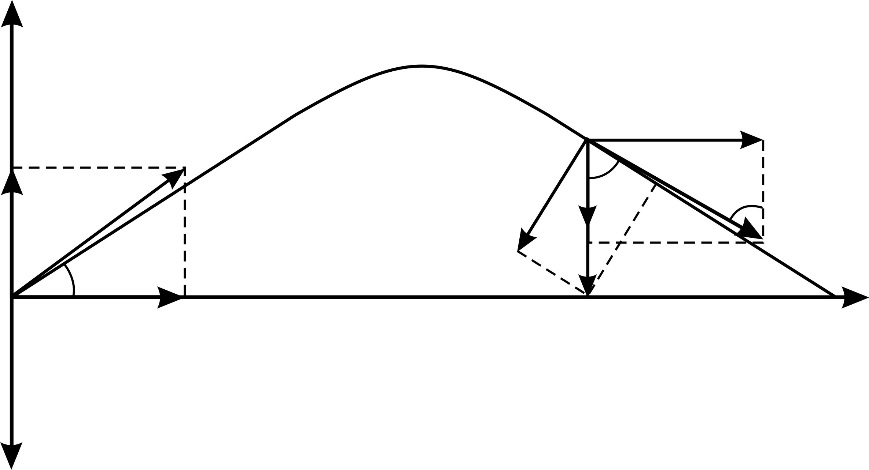
В данном случае размерами тела можно пренебречь и принять его за материальную точку. Если не учитывать сопротивление воздуха, то в поле силы тяжести тело движется с постоянным ускорением 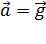 , направленным вертикально вниз (рис. 2). Движение тела криволинейное, сложное и характеризуется системой уравнений:
, направленным вертикально вниз (рис. 2). Движение тела криволинейное, сложное и характеризуется системой уравнений:
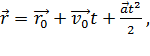
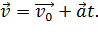 (1) Это движение можно представить как совокупность двух прямолинейных движений: горизонтального – по оси x, и вертикального – по оси y. Законы этих прямолинейных движений получим, проецируя на оси х и у уравнения (1). Запишем проекцию левой и правой части уравнений (1) на ось x:
(1) Это движение можно представить как совокупность двух прямолинейных движений: горизонтального – по оси x, и вертикального – по оси y. Законы этих прямолинейных движений получим, проецируя на оси х и у уравнения (1). Запишем проекцию левой и правой части уравнений (1) на ось x:
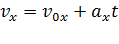 ;
; 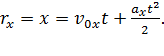
Так как проекция ускорения 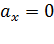 , а начальная скорость
, а начальная скорость 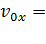
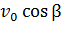 , то
, то
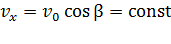 ,
, 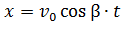 , (2)
, (2)
т. е. движение вдоль оси х равномерное. Аналогично запишем для оси у:
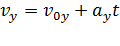 ,
, 
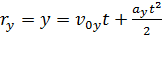 . (3)
. (3)
По рис. 2 видно, что 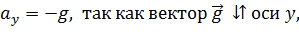 а скорость
а скорость 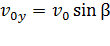 ; поэтому уравнения (3) принимают следующий вид:
; поэтому уравнения (3) принимают следующий вид:
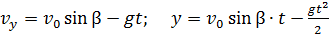 . (4)
. (4)
Следовательно, движение тела вдоль оси у равнопеременное: с постоянным ускорением 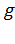 .
.
1) Найдем уравнение траектории в виде 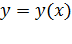 . Для этого из уравнения (2) выразим время
. Для этого из уравнения (2) выразим время 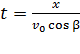 и подставим его в уравнение (4):
и подставим его в уравнение (4):
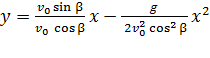 , или
, или 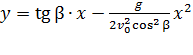 .
.
После вычисления коэффициентов при переменной x получаем уравнение траектории в виде:
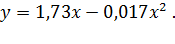
Это уравнение параболы, ветви которой направлены вниз (см. рис. 2).
2) Время движения тела 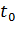 состоит из двух интервалов времени: времени подъема
состоит из двух интервалов времени: времени подъема 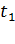 и равного ему времени падения
и равного ему времени падения 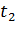 , так как падение и подъем тела происходили с одинаковым ускорением g. Время подъема может быть найдено из условия
, так как падение и подъем тела происходили с одинаковым ускорением g. Время подъема может быть найдено из условия 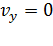 в наивысшей точке траектории, т. е., в соответствии с уравнением (4):
в наивысшей точке траектории, т. е., в соответствии с уравнением (4): 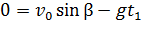 , откуда время
, откуда время 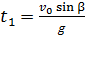 , а время движения тела
, а время движения тела 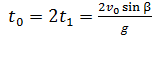 .
.
Вычисляем по этой формуле: 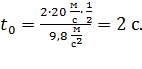
Видим, что заданное время 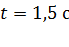 меньше, чем
меньше, чем 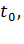 но больше времени движения до вершины параболы
но больше времени движения до вершины параболы 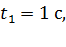 следовательно, заданная точка находится на нисходящей ветви параболы.
следовательно, заданная точка находится на нисходящей ветви параболы.
3) Модуль скорости движения тела выразим через проекции:
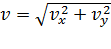 .
.
Подставляя значения проекций скорости по формулам (2) и (4), получаем
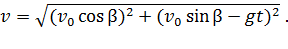
Вычисляем: 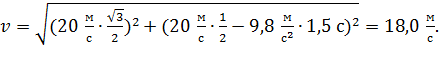
Тангенциальное 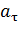 и нормальное
и нормальное 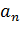 ускорения могут быть определены двумя способами: аналитическим – по определительным формулам, и графическим – этот способ применим в данном решении.
ускорения могут быть определены двумя способами: аналитическим – по определительным формулам, и графическим – этот способ применим в данном решении.
Изобразим на рис. 2 в момент времени 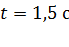 вектор скорости тела и его проекции
вектор скорости тела и его проекции 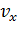 и
и 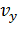 . Далее изобразим в этот же момент времени вектор полного ускорения
. Далее изобразим в этот же момент времени вектор полного ускорения 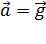 и разложим его на составляющие
и разложим его на составляющие 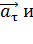
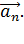 Для этого проведем касательную к траектории (по ней направлен вектор скорости) и нормаль – перпендикулярно касательной. Чтобы найти составляющие
Для этого проведем касательную к траектории (по ней направлен вектор скорости) и нормаль – перпендикулярно касательной. Чтобы найти составляющие 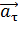 и
и 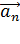 , с конца вектора
, с конца вектора 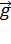 опустим перпендикуляры на касательную и нормаль к траектории. Из полученного треугольника ускорений находим значения ускорений
опустим перпендикуляры на касательную и нормаль к траектории. Из полученного треугольника ускорений находим значения ускорений
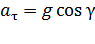 ;
; 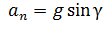 . (5)
. (5)
Так как угол 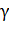 есть и в треугольнике скоростей, запишем значения
есть и в треугольнике скоростей, запишем значения 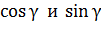 через проекции и модуль скорости:
через проекции и модуль скорости:
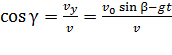 ;
; 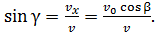
Вычислим 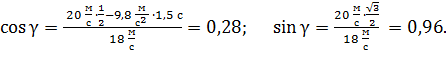
Результат расчета ускорений по формулам (5):
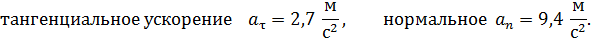
Радиус кривизны траектории в точке A, где находилось тело в момент 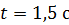 ,находим из формулы нормального ускорения:
,находим из формулы нормального ускорения:
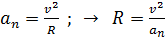 ; вычисляем
; вычисляем 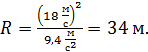
Задача 2. Материальная точка движется по окружности радиусом 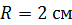 . Зависимость пути от времени дается уравнением
. Зависимость пути от времени дается уравнением 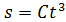 , где
, где 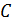 = 0,1
= 0,1 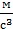 . Определите нормальное и тангенциальное ускорение точки в момент, когда линейная скорость точки
. Определите нормальное и тангенциальное ускорение точки в момент, когда линейная скорость точки 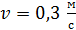 .
.
Дано Решение
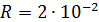 м; Найдем нормальное ускорение по формуле
м; Найдем нормальное ускорение по формуле
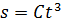 ;
; 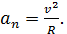
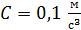 ; Вычислим
; Вычислим 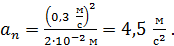
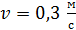 . Запишем определительную формулу тангенциального
. Запишем определительную формулу тангенциального
D OJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYA CAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYA CAAAACEAKhxP5OQBAADdAwAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAU AAYACAAAACEAL+VUrNsAAAAGAQAADwAAAAAAAAAAAAAAAAA+BAAAZHJzL2Rvd25yZXYueG1sUEsF BgAAAAAEAAQA8wAAAEYFAAAAAA== " strokecolor="black [3040]"/> 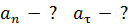 ускорения
ускорения
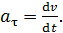 (1)
(1)
Найдем модуль скорости по формуле 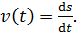 (2)
(2)
Дифференцируя зависимость пути от времени, получаем
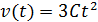 . (3)
. (3)
В соответствии с формулой (1) величина 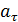 равна производной от функции
равна производной от функции 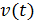 ; с учетом выражения (3) находим
; с учетом выражения (3) находим
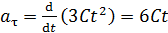 , (4)
, (4)
где t – момент времени, в который скорость стала равна 0,3 м/с. Находим это время из формулы (3):
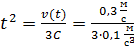
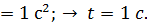
Вычисляем тангенциальное ускорение по формуле (4):
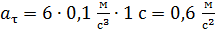 .
.
Задача 3. Материальная точка вращается вокруг неподвижной оси по закону 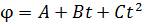 , где
, где 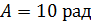 ,
, 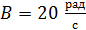 ,
, 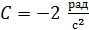 . Определите полное ускорение точки, находящейся на расстоянии
. Определите полное ускорение точки, находящейся на расстоянии 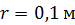 от оси вращения, для момента времени
от оси вращения, для момента времени 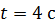 .
.
Дано 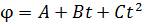 ; ; 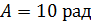 ; ; 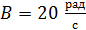 ; ; 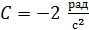 ; ; 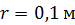 ; ; 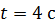 . . 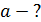
|
|||
Решение
Полное ускорение 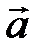 материальной точки, движущейся по криволинейной траектории, может быть найдено как векторная сумма тангенциального ускорения
материальной точки, движущейся по криволинейной траектории, может быть найдено как векторная сумма тангенциального ускорения 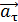 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения 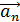 , направленного к центру кривизны траектории:
, направленного к центру кривизны траектории:
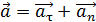 .
.
Так как векторы ускорений 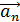 и
и 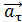 взаимно перпендикулярны (рис. 3), то модуль ускорения
взаимно перпендикулярны (рис. 3), то модуль ускорения
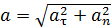 . (1) Нормальное и тангенциальное ускорения точки вращающегося тела выражаются формулами
. (1) Нормальное и тангенциальное ускорения точки вращающегося тела выражаются формулами
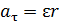 ,
, 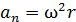 ,
,
где 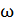 – угловая скорость;
– угловая скорость; 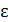 – угловое ускорение тела.
– угловое ускорение тела.
Подставляя выражения 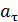 и
и 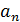 в формулу (1), находим полное ускорение вращающейся материальной точки
в формулу (1), находим полное ускорение вращающейся материальной точки
Рис. 3 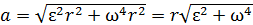 . (2)
. (2)
Угловую скорость 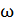 найдем, взяв первую производную от угла поворота по времени:
найдем, взяв первую производную от угла поворота по времени:
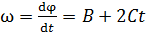 .
.
Вычислим угловую скорость в момент времени 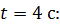
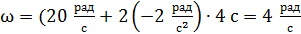 .
.
Угловое ускорение находим, взяв первую производную от угловой скорости по времени:
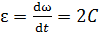 ; вычислим
; вычислим 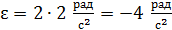 .
.
Подставляя значения 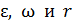 в формулу (2), получаем величину полного ускорения материальной точки:
в формулу (2), получаем величину полного ускорения материальной точки:
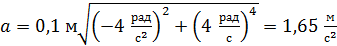 .
.
Дата добавления: 2016-10-07; просмотров: 4190;


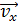
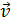
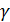
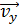
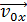
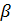
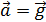
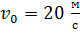 ;
;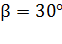 ;
;