Работа и механическая энергия

Работа – это одна из форм передачи энергии от одних тел к другим. Поэтому, при решении задач следует помнить, что работа совершается за счет убыли энергии.

В зависимости от условий задачи рассматривают два основных пути определения работы.

1. Известна сила F, под действием которой перемещается тело. В этом случае работа на участке траектории от точки 1 до точки 2 определяется по формуле:

;

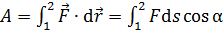где 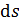– малое перемещение тела, на котором величину силы можно считать постоянной; 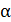– угол между направлением действия силы и направлением перемещения.

Если сила постоянна (не изменяется ее величина и угол α), то формула для вычисления работы принимает простой вид:

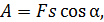
где 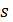– путь, пройденный телом под действием силы .

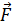2. Сила неизвестна, но известна механическая энергия тела 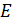. В этом случае работу вычисляют как приращение энергии тела, т. е. как разность энергии тела в конечном и начальном состояниях:

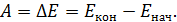
В механике рассматривают механическую энергию, складывающуюся из кинетической 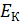и потенциальной энергии .

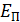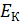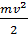Кинетическая энергия – это энергия, зависящая от скорости движения тела. При поступательном движении тела массой m со скоростью v его кинетическая энергия равна . При вращательном движении тела, имеющего момент инерции I, c угловой скоростьюw его кинетическая энергия равна 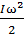. При одновременном участии тела в обоих видах движения кинетическая энергия определяется формулой

.

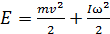Потенциальная энергия – энергия, обусловленная взаимодействием тел и зависящая от положения тел или их частей относительно друг друга. Потенциальной энергией обладают все упруго деформированные тела, например, растянутая или сжатая пружина, а также все тела, которые притягиваются или отталкиваются друг от друга: Земля и другие планеты, взаимодействующие с Солнцем, молекулы, заряженные тела. Потенциальная энергия всегда взаимная, она относится к обоим взаимодействующим телам.

Для тела массой m, поднятого над поверхностью Земли на высоту h, потенциальная энергия 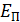определяется по формуле

.

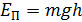Эта формула справедлива только для случая, когда 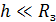, где 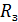– радиус Земли, и если за нулевой уровень 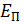принимают энергию тела на поверхности Земли.

Для упруго деформированной пружины (пластины) и т. п.

,

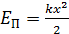где k – коэффициент упругости или жесткость пружины; 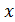– величина деформации: удлинение или сжатие тела.

Вид функции потенциальной энергии находят, вычисляя неопределенный интеграл:

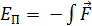
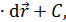
где 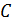– постоянная интегрирования, зависящая от выбора нулевого уровня 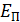. Используя эту формулу для расчета 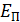любого тела и Земли и учитывая, что сила их взаимного притяжения 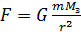, получаем

,

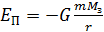где 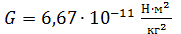– гравитационная постоянная; m и 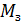– массы тела и Земли; r – расстояние от центра Земли до центра масс тела. Формула дает значение 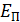тела относительно его положения в бесконечности, в котором .

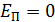Таким образом, потенциальная и кинетическая энергия тела являются величинами относительными, т. е. их численное значение зависит от выбора системы отсчета.

Итак, на совершение работы тратится энергия. Но не вся затраченная энергия идет на полезную работу; часть ее расходуется на преодоление сил трения. Механизмы, с помощью которых совершается работа, характеризуют коэффициентом полезного действия (КПД) h, равным отношению полезной работы 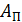ко всей совершенной работе 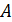, т. е. к затраченной энергии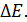

.

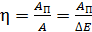Быстроту совершения любой работы характеризуют мощностью. Следует различать среднюю мощность 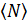и мгновенную мощность 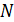. Среднюю мощность рассчитывают по формуле

,

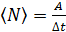где 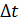– интервал времени, в течение которого совершена работа .

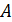Мгновенную мощность определяют по формулам

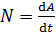и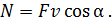

Здесь 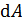– элементарная работа, совершаемая силой F за бесконечно малый промежуток времени 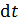; 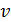– скорость движения тела.

Законы сохранения

Всякая система при движенииизменяет свое состояние, при этом изменяются значения параметров, характеризующих состояние системы. Однако существуют такие величины – функции состояния, которые обладают важным свойством оставаться с течением времени неизменными, если соблюдены определенные условия. Среди этих величин наиболее важную роль в механике играют импульс, момент импульса и энергия механической системы.