Динамика вращательного движения

При решении рассматриваемой ниже группы задач в зависимости от условий необходимо бывает найти как кинематические параметры движения – скорость и ускорение движущихся тел, пройденный ими путь, так и динамические характеристики – силу и момент силы, а также физические величины, характеризующие участвующие в движении тела: массу и момент инерции.

Основной закон динамики вращательного движения:

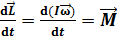, или ,

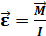где 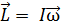– вектор момента импульса тела; 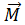– вектор момента силы; I – момент инерции тела, 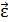– угловое ускорение тела.

Момент инерции тела приближенно находится как сумма моментов инерции материальных точек, составляющих тело:

.

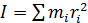Здесь 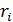– расстояние отдельных точек от оси или центра вращения; 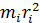– момент инерции i-той материальной точки массой .

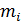В случае непрерывного распределения масс эта сумма сводится к интегралу по всей массе тела:

.

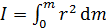Таким способом вычисляют моменты инерции разных тел. Приведем значения моментов инерции некоторых тел массой m (тела однородные):

а) полый тонкостенный цилиндр и обруч радиуса R относительно его оси симметрии:

;

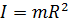б) сплошной цилиндр и диск радиуса R относительно его оси симметрии:

;

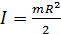в) шар радиуса R относительно оси, проходящей через его центр:

.

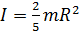Теорема Штейнера позволяет найти момент инерции I некоторого тела массой m относительно произвольной оси:

,

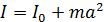если известен момент инерции I₀ этого тела относительно оси, проходящей через центр масс тела параллельно произвольной оси, находящейся на расстоянии 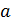от нее.

Момент силы 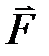относительно оси z (проекция вектора 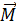на ось z)

,

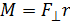
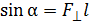где 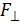– проекция силы на плоскость, перпендикулярную оси вращения z, r – величина радиуса-вектора, проведенного из точки О на оси Z к точке приложения силы; l – плечо силы, – это кратчайшее расстояние (по перпендикуляру) от оси вращения до линии действия силы.