Кинематика поступательного и вращательного движения
При рассмотрении задач данного раздела вводят понятие материальной точки (МТ). За материальную точку может быть принято любое тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь. Линия, описываемая материальной точкой в пространстве при ее движении, называется траекторией. Уравнение траектории для плоского движения имеет вид
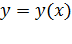 .
.
Движение материальной точки в пространстве определяется законом движения, который для МТ может быть задан в виде трех скалярных уравнений:
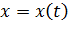 ,
,
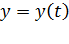 ,
,
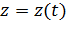 ,
,
либо эквивалентным векторным уравнением:
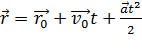 .
.
Быстроту движения материальной точки характеризуют средней скоростью
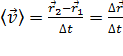 или
или 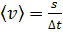 ,
,
где s – путь, пройденный за время 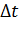 , и мгновенной скоростью
, и мгновенной скоростью
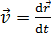 ,
,
которая может быть записана, как любой вектор, в координатной форме:
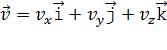 , а модуль
, а модуль 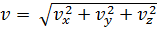 ,
,
где проекции скорости 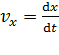 ;
; 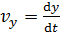 ;
; 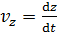 .
.
Быстроту изменения скорости при неравномерном движении характеризует ускорение: среднее ускорение
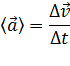
и мгновенное ускорение
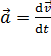 .
.
С другой стороны,
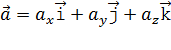 ,
,
где проекции вектора ускорения равны соответствующим производным по времени от проекций скорости:
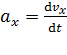 ;
; 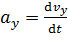 ;
; 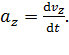
В криволинейном движении осями координат могут быть касательная к траектории движения материальной точки и нормаль к ней. Орты осей в этом случае 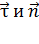 . При этом полное ускорение
. При этом полное ускорение
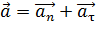 , а его модуль
, а его модуль 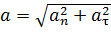 ,
,
где тангенциальное ускорение 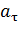 характеризует быстроту изменения модуля скорости и направлено по касательной к траектории:
характеризует быстроту изменения модуля скорости и направлено по касательной к траектории:
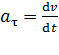 , вектор
, вектор 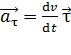 ;
;
нормальное ускорение характеризует быстроту изменения направления скорости и направлено по нормали к центру кривизны траектории:
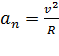 , вектор
, вектор 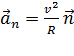 .
.
Здесь R – радиус кривизны траектории.
Движение материальной точки по окружности характеризуют угловой скоростью 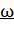
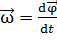 ,
, 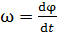
и угловым ускорением 
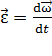 ,
, 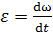 .
.
Угловые и линейные величины связаны следующими соотношениями:
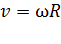 ;
;
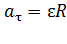 ;
;
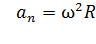 .
.
Зная зависимость 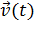 или
или 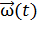 , можно найти
, можно найти 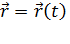 и
и 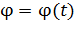 :
:
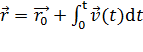 ,
, 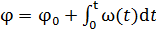 .
.
Например, для равнопеременного поступательного движения ( 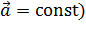 и равнопеременного вращения (
и равнопеременного вращения ( 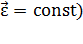 ) получаем:
) получаем:
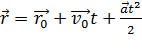 ,
, 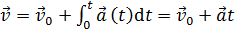 ;
;
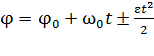 ,
, 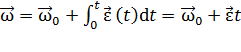 .
.
Дата добавления: 2016-10-07; просмотров: 1701;











