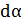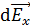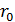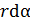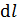Расчет напряженности и потенциала электростатического поля

С помощью принципа суперпозиции

План решения задач

1.Изобразите на рисунке схему расположения точечных зарядов или заряженных тел в соответствии с условием задачи. На схеме: 1) покажите знаки зарядов и их символы с индексом, равным номеру заряда; 2) обозначьте точку, в которой нужно определить величины напряженности и потенциала ЭСП, например, точка .

2. Запишите принцип суперпозиции для расчета напряженности поля в следующем виде:

а) если ЭСП создается системой точечных зарядов или заряженных тел, то

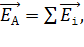(1)

где 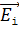– вектор напряженности поля i-того заряда или заряженного тела; число слагаемых в уравнении (1) равно числу зарядов, создающих поле;

б) если ЭСП создается зарядом, распределенным равномерно, например, по длине заряженного тела, тогда

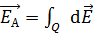, (2)

где 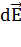– бесконечно малый вектор напряженности, создаваемый элементарным зарядом 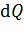, выделенным на заряженном теле.

3. Так как в уравнениях (1) и (2) записана сумма векторов, которые следует складывать геометрически, то необходимо показать на рисунке направления суммируемых векторов. Для этого мысленно помещают в исследуемую точку поля пробный положительный заряд 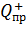и показывают направление сил 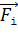, действующих на этот пробный заряд со стороны каждого i-того заряда (естественно, что векторы всех сил, приложенных к заряду 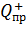, начинаются в точке ). Поскольку векторы напряженности 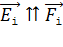, то обозначают изображенные векторы символами 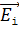, где индекс величины 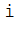совпадает с индексом заряда, создающего поле. Аналогично определяют направление векторов 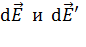от бесконечно малых точечных зарядов 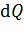и 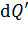, которые выбирают, как правило, в точках заряженного тела, распложенных симметрично относительно его оси симметрии.

4. Сложение двух векторов 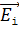обычно выполняют с помощью правила параллелограмма (или треугольника); при этом модуль определяемого результирующего вектора находят по теореме косинусов. Если число складываемых векторов равно трем и более, в том числе и при суммировании бесконечно малых векторов 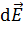, то находят проекции результирующего вектора 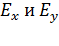на координатные оси 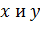, проецируя на эти оси каждый из суммируемых векторов. В этом случае модуль результирующего вектора определяют с помощью теоремы Пифагора: 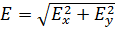. Оси направляют таким образом, чтобы удобно было записывать проекции 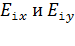, т. Е. чтобы были известны углы, образованные векторами 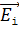с осями координат. Либо одну из осей проводят по предполагаемому направлению результирующего вектора 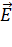, которое можно определить, используя симметрию в расположении зарядов, если таковая имеется.

5. Потенциал электростатического поля в исследуемой точке находят также с помощью принципа суперпозиции:

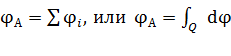, (3)

алгебраически суммируя потенциалы, которые создаются в данной точке заряженными телами, в том числе, точечными зарядами 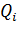или бесконечно малыми точечными зарядами 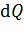. При этом суммировании знаки потенциалов 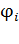равны знакам соответствующих -тых зарядов, в частности, отрицательный заряд создает в точке электростатическое поле с отрицательным значением потенциала.

Задача 4.Два точечных заряда 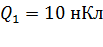и 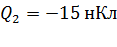расположены в двух вершинах равностороннего треугольника со стороной 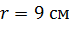. Определите напряженность 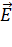электростатического поля и его потенциал в точке А, находящейся в третьей вершине.

Дано Решение

; ; ;

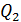
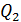
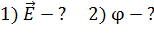
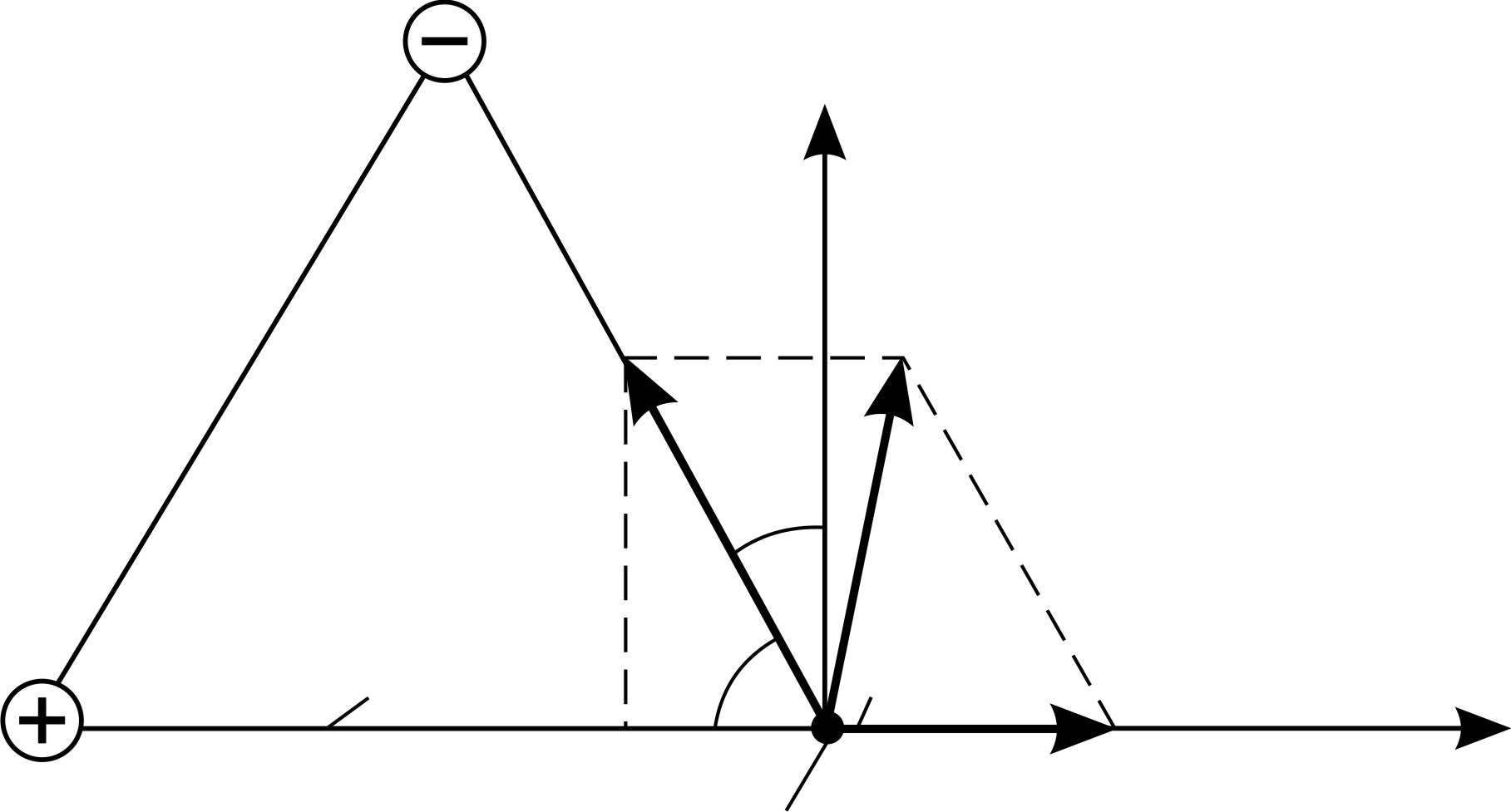
Рис. 11

Расположение зарядов 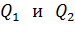относительно точки показано на рис. 11.
1) Для расчета напряженности 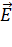используем принцип суперпозиции ЭСП в виде:

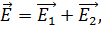(1)

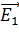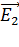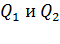где и – напряженности полей, создаваемых в точке зарядами соответственно.

Чтобы определить направление складываемых векторов, в точку мысленно помещаем пробный заряд 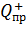и рассматриваем действующие на него силы: первый заряд 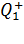отталкивает заряд 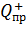силой 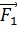, направленной по линии соединяющей заряды 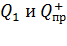, а второй – отрицательный заряд 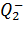притягивает к себе положительный заряд 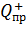силой 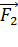, также направленной по линии, соединяющей заряды 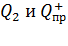. Напряженность поля, создаваемого i-тым зарядом, 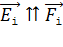, т. е. совпадает по направлению с соответствующей силой.

Модуль результирующего вектора можно найти любым из двух способов: а) по теореме косинусов:

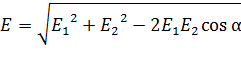, (2)

где напряженности ЭСП, создаваемого точечными зарядами 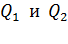в точке , находящейся на расстоянии от каждого заряда:

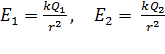; (3)

б) по проекциям принципа суперпозиции (1) на координатные оси :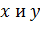

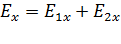; (4)

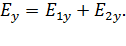(5)

Ось направляем вдоль вектора 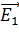, при этом вектор 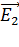образует известные углы 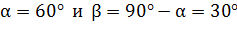с осями 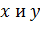(см. рис. 11). Следовательно, проекции результирующего вектора : 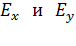, – на координатные оси 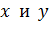, будут определяться выражениями:

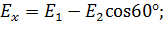
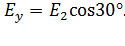
В результате

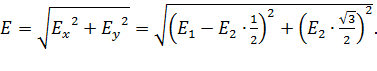(6)

Подставим формулы (3) для напряженностей 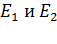в выражение (6) и, вынося одинаковый сомножитель 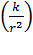за скобки и из радикала, получим следующую расчетную формулу величины :

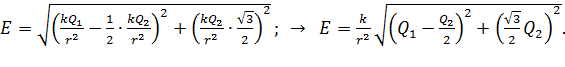(7)

Вычисляем по формуле (7) напряженность электростатического поля в точке , заметив, что при этом нужно подставлять модуль отрицательного заряда 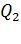, поскольку знак его уже учтен в направлении вектора :

.

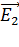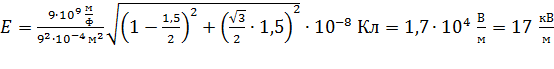2) Расчет потенциала 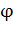в точке электростатического поля выполняем, используя принцип суперпозиции:

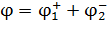, (8)

где потенциалы ЭСП, созданного точечными зарядами 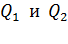в точке , находящейся на расстоянии от каждого заряда, определяются следующими формулами:

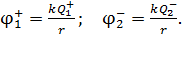(9)

С учетом этих формул равенство (8) запишется в виде:

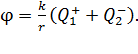(10)

В полученной расчетной формуле каждый заряд записывается с его знаком, так как только в этом случае получим алгебраическую сумму потенциалов полей, создаваемых отдельными зарядами. Вычислим потенциал в исследуемой точке электростатического поля по формуле (10):

.

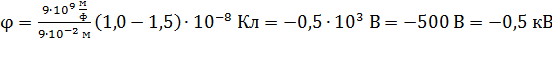Задача 5.Четыре точечных заряда 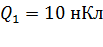, , 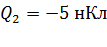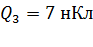и 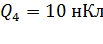, расположены в вершинах квадрата со стороной 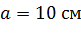. Определите напряженность 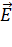электростатического поля и его потенциал 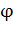в точке 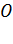пересечения диагоналей квадрата.

Дано Решение

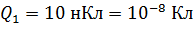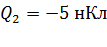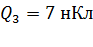; ; ; ; . 1) 2)

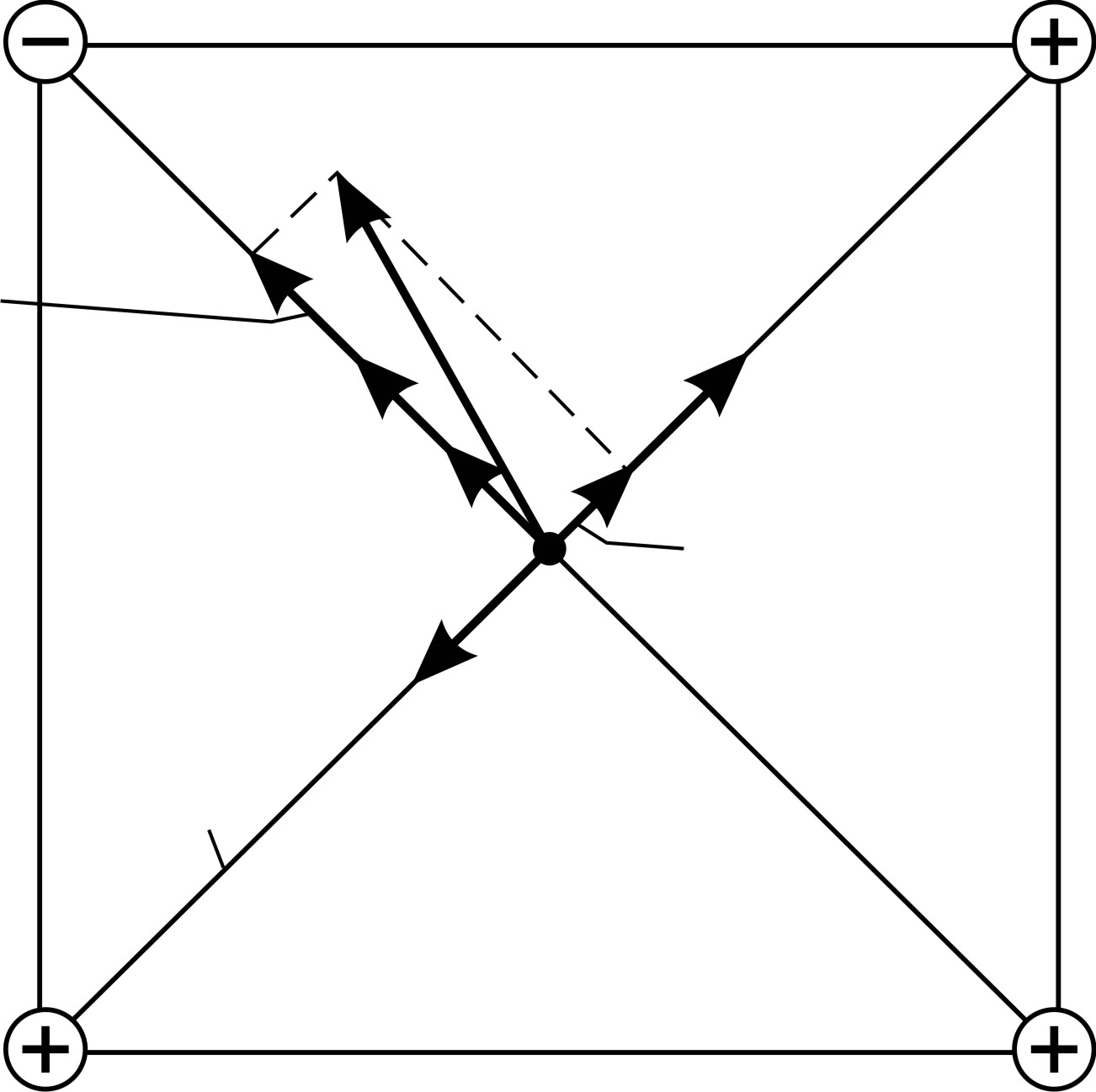
Рис. 12

Расположение зарядов в вершинах квадрата показано на рис. 12.

1) Для расчета напряженности вектора 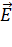в точке 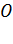используем принцип суперпозиции электростатического поля в виде:

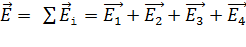, (1)

где 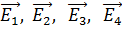– напряженности полей, создаваемых в точке О зарядами 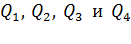соответственно.

Для определения направления суммируемых векторов в исследуемую точку поля О мысленно помещаем пробный положительный заряд 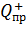и рассматриваем действующие на него силы: каждая сила направлена по линии, соединяющей пробный заряд и заряд 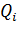и приложена к пробному заряду в точке 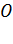. При этом положительные заряды 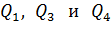отталкивают от себя 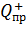, а отрицательный заряд 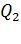притягивает к себе 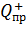. По направлениям этих сил 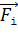, действующих на пробный заряд, направлены соответствующие векторы напряженностей 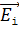(см. рис. 12).

Векторы, направленные по одной прямой (коллинеарные) складываем попарно:

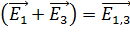; так как 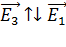, то модуль вектора 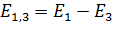; (2)

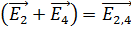; так как 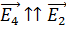, то модуль вектора 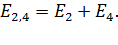(3)

Учитывая эти равенства, принцип суперпозиции (1) перепишем в следующем виде:

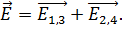(4)

Так как векторы 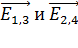взаимно перпендикулярны, то их складываем по правилу параллелограмма (треугольника); при этом модуль результирующего вектора определяем с помощью теоремы Пифагора:

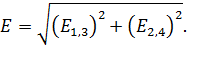
С учетом формул (2) и (3) модуль напряженности ЭСП в точке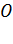

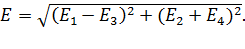(5)

Напряженность ЭСП, создаваемого точечным зарядом :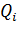

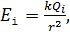(6)

где – расстояние от точечного заряда до точки 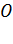в ЭСП. Подставляя напряженности 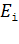согласно формуле (6) в равенство (5) и вынося одинаковый сомножитель 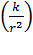за скобки и из радикала, получим расчетную формулу для величины напряженности в следующем виде:

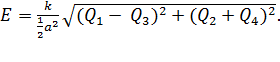(7)

Вычисляя по формуле (7) напряженность поля в точке 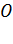, заметим, что при этом в формулу следует подставить модуль отрицательного заряда 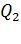, так как знак его уже учтен в изображении вектора 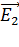на рис. 12.

.

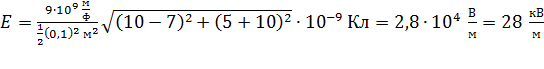2) Рассчитываем потенциал 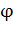электростатического поля в точке 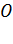с помощью принципа суперпозиции:

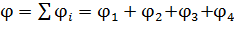, (8)

где 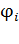– потенциал поля, создаваемого точечным зарядом 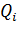в точке 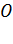, находящейся на расстоянии от заряда:

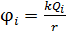. (9)

Подставляя формулы (9) в равенство (8), получаем следующую расчетную формулу для потенциала ЭСП в точке :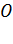

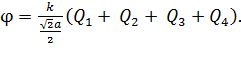(10)

Здесь заряды записываются с их знаками: так как отрицательный заряд 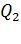создает поле с отрицательным потенциалом, то 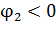. Вычисляем потенциал точки 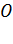электростатического поля по формуле (10):

.

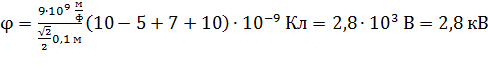Задача 6.В вершинах правильного шестиугольника со стороной 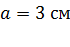находятся четыре положительных и два отрицательных точечных заряда; все заряды имеют одинаковый модуль 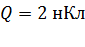. Определите напряженность 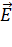электростатического поля и потенциал 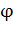в центре шестиугольника при трех различных вариантах расположения этих зарядов.

Дано Решение

; ; ;

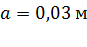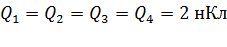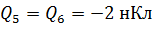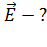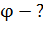в вариантах 1, 2 и 3.

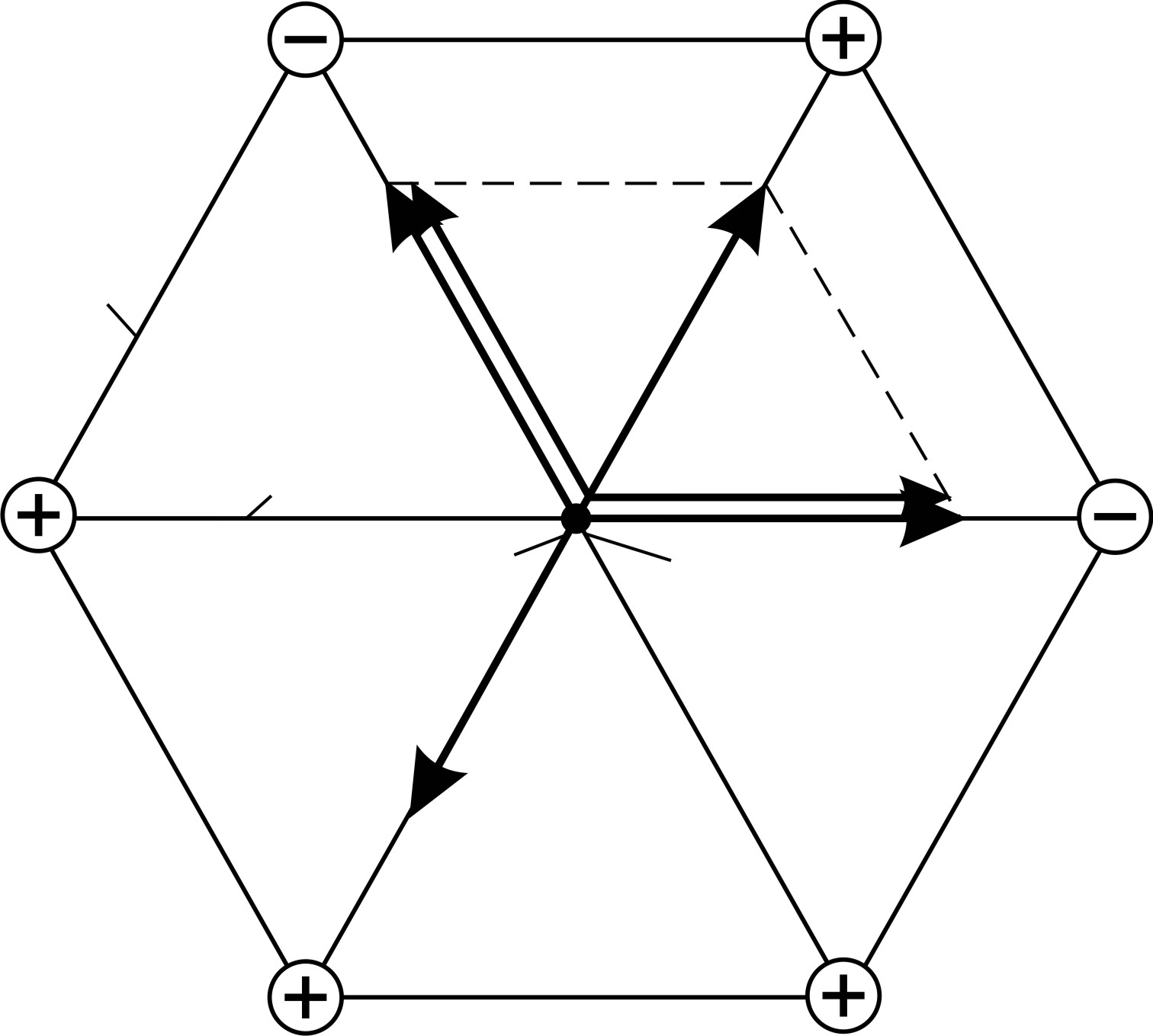
1) Рис. 13

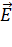Для расчета в центре шестиугольника (в точке ) напряженности электростатического поля, создаваемого системой из шести точечных зарядов, используем принцип суперпозиции:

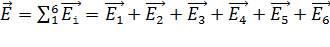, (1)

где 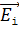– вектор напряженности поля, создаваемого в точке i-тым зарядом ( 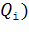; индекс вектора 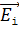совпадает с индексом заряда .

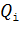Чтобы определить направления суммируемых векторов, в точку мысленно поместим пробный положительный заряд 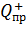и покажем направления действующих на него сил со стороны i-тых зарядов: все силы направлены вдоль линий, соединяющих пробный заряд 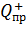с зарядом 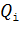. При этом положительные заряды 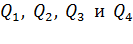отталкивают от себя пробный заряд, а отрицательные 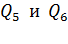–притягивают к себе 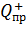. По направлениям сил 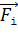, действующих на пробный заряд, направлены соответствующие векторы напряженности 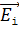(рис. 13).

Векторы, направленные вдоль одной прямой (коллинеарные), складываем попарно, учитывая, что модули всех векторов одинаковы:

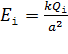. (2)

С учетом направления векторов 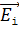в точке (см. рис. 13), перепишем равенство (1) в виде:

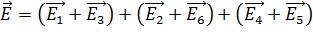. (1а)

Так как вектор 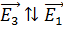, то их сумма 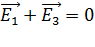; сумма сонаправленных векторов: 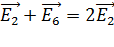, и .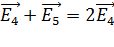

С учетом этих соотношений принцип суперпозиции (1а) перепишем в следующем виде:

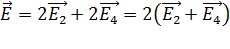. (3)

Векторы 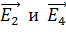складываем по правилу параллелограмма (треугольника). Так как диагонали шестиугольника разделяют его площадь на равносторонние треугольники, то по рис. 13 видно, что 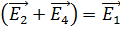. Тогда результирующий вектор напряженности ЭСП в точке

.

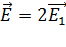С учетом формулы (2) модуль этого вектора

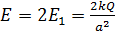. (4)

Вычисляем напряженность ЭСП в исследуемой точке :

.

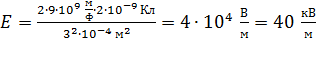Потенциал электростатического поля в точке определяется по принципу суперпозиции как алгебраическая сумма потенциалов полей, создаваемых шестью точечными зарядами:

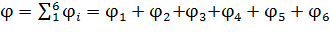, (5)

где 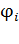– потенциал поля, создаваемого точечным зарядом 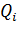в точке , находящейся на расстоянии 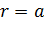от заряда; он определяется следующей формулой:

.

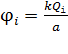Поскольку все заряды одинаковы по модулю и находятся на одинаковом расстоянии от исследуемой точки поля , то слагаемые в уравнении (5) различаются только знаком; при этом, согласно условию задачи, имеем

;

.

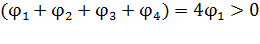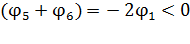В соответствии с уравнением (5) сумма этих потенциалов

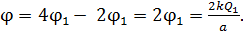(6)

Величина 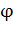, определяемая уравнением (6), не изменяется при любом варианте размещения данных зарядов в вершинах шестиугольника.

Вычисляем потенциал электростатического поля в точке :

.

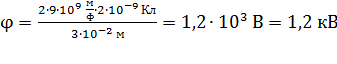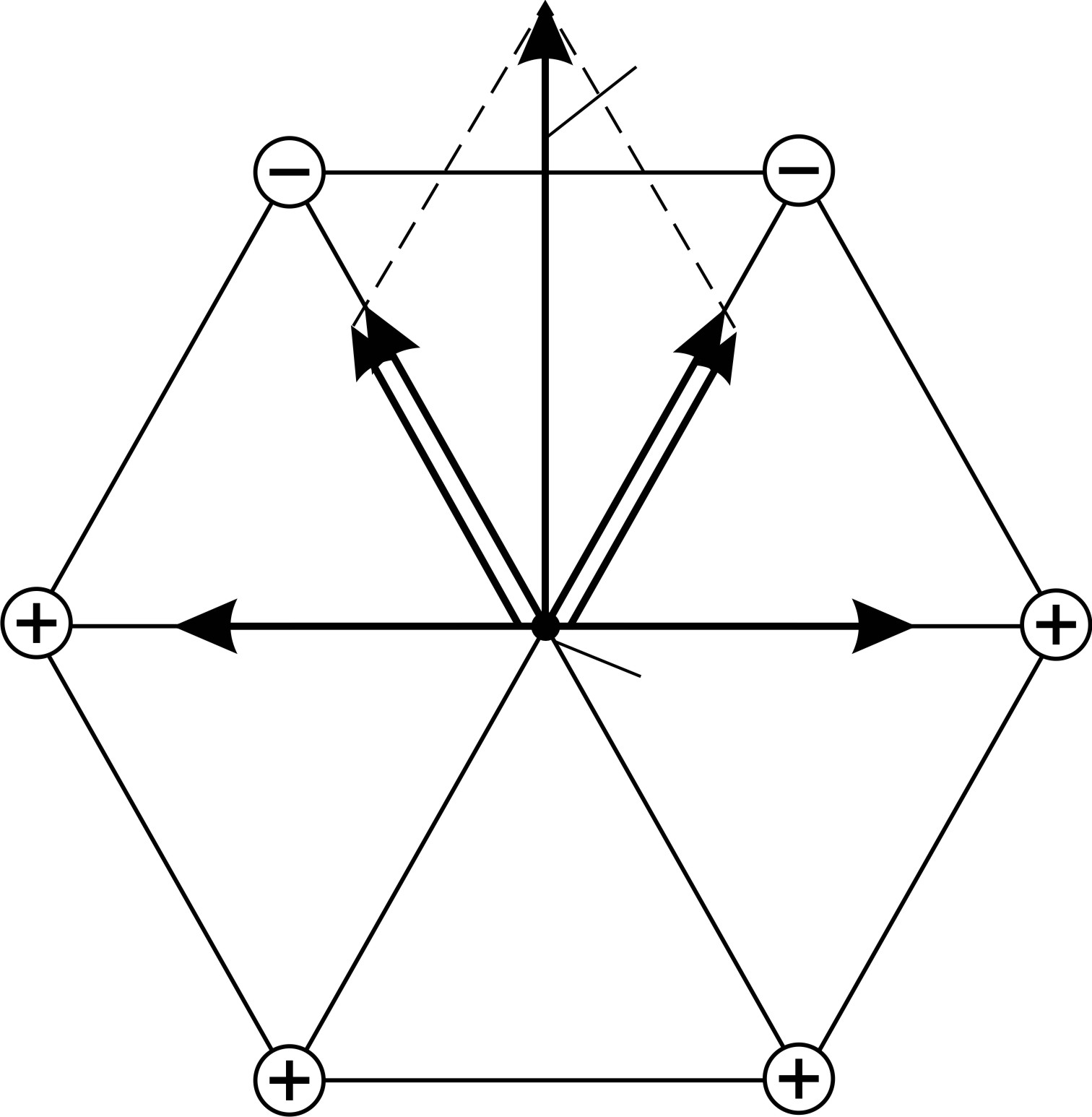
2) Рис. 14

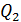
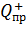Для второго варианта размещения зарядов на рис. 14 также покажем векторы всех сил, действующих на пробный заряд , помещенный в точку , и 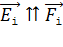. По принципу суперпозиции полей (1) складываем векторы напряженности 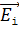, как рассмотрено выше, т. е. попарно:

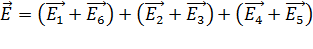
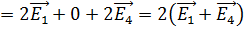, (7)

где модуль напряженности 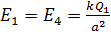, – в соответствии с формулой (2).

Модуль результирующего вектора 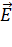определяем из треугольника на рис. 14 по теореме косинусов, в соответствии с уравнением (7):

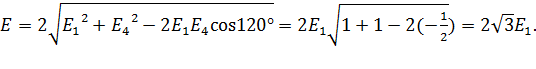(8)

Сравнивая формулы (8) и (4), отмечаем, что в данном варианте размещения зарядов напряженность в 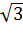раз больше, чем в первом случае:

.

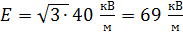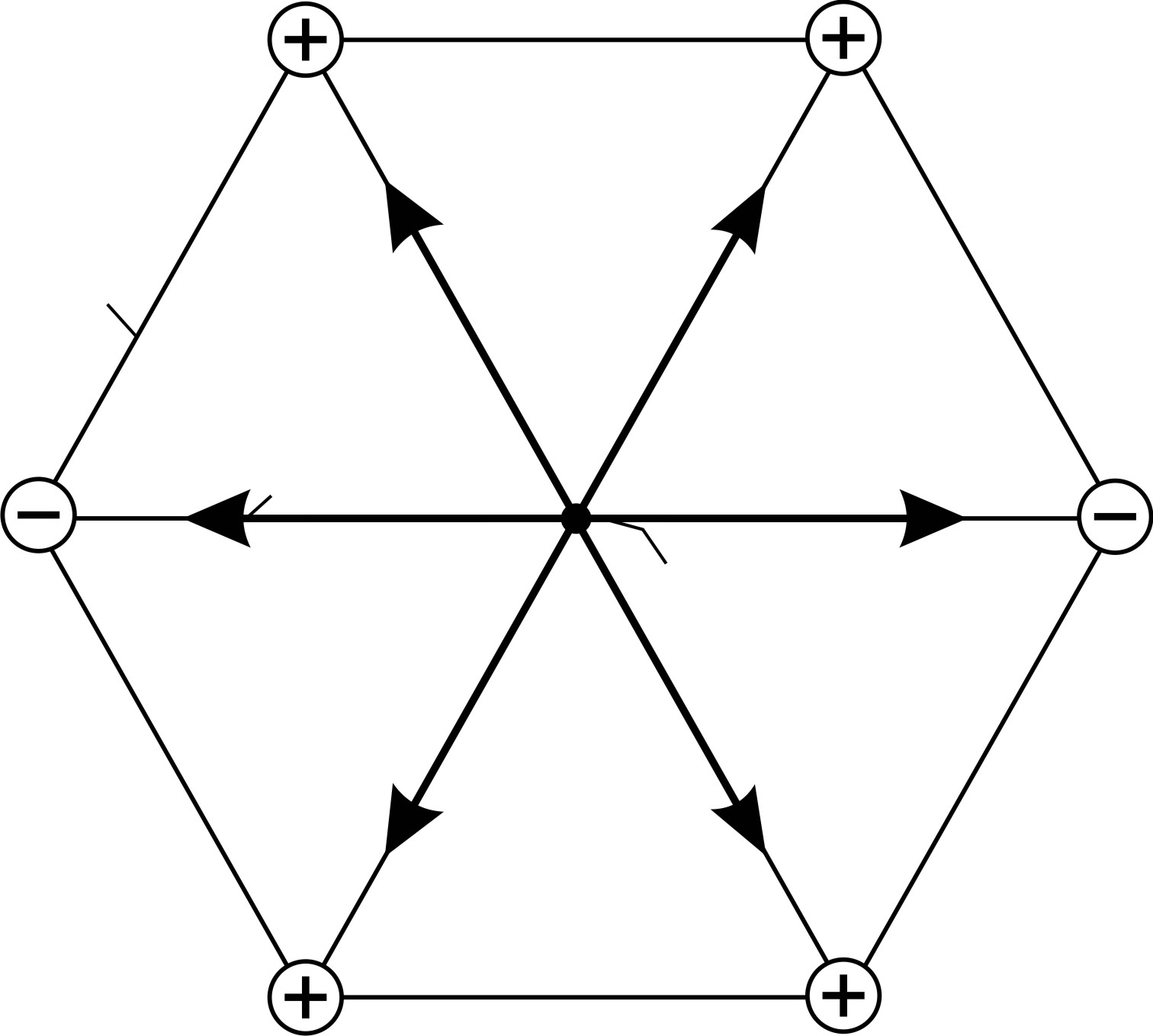
3) Рис. 15

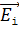Направления напряженностей полей, созданных в точке каждым точечным зарядом, показаны на рис. 15. Складываем векторы 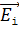, согласно принципу суперпозиции ЭСП (1); при этом выделяем пары векторов, которые направлены по одной линии:

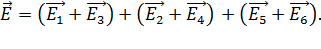
В последнем уравнении векторы, заключенные в скобки, равны по модулю и противоположны по направлению; следовательно, их сумма равна нулю. Соответственно, и результирующий вектор 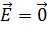, так как поля, созданные зарядами одинакового знака, в точке взаимно компенсируются.

Задача 7.Электростатическое поле создается нитью длиной 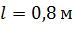, несущей заряд 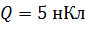, равномерно распределенный по длине нити. Определите напряженность 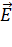и потенциал 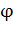в точке , лежащей на продолжении нити на расстоянии 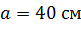от ближайшего ее конца.

Дано Решение

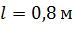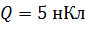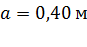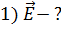; ; . 2)

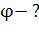
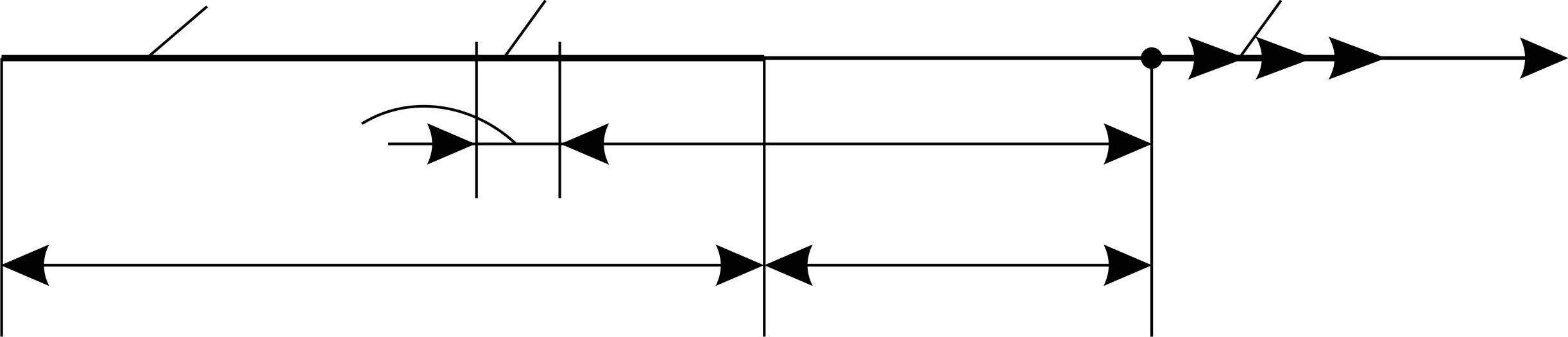
) Рис. 16

1) Размер заряженного тела – длина нити , соизмерим с расстоянием от нити до исследуемой точки поля , следовательно, заряд нити не является точечным. В таких случаях мысленно разделяют заряд нити на элементарные заряды 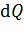и суммируют создаваемые ими в точке поля напряженностью 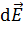(рис. 16).

Чтобы определить направление векторов 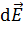в точке , мысленно поместим в эту точку пробный положительный заряд 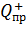и покажем векторы сил 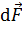, действующих со стороны элементарных зарядов нити 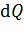на пробный заряд. Векторы 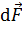направлены по линии, соединяющей заряды 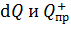, а векторы 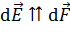, следовательно, все бесконечно малые векторы напряженности 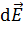полей элементарных зарядов нити 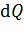направлены вдоль оси , т. е. параллельны друг другу.

Результирующий вектор 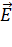, согласно принципу суперпозиции:

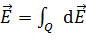, (1)

в этом случае направлен вдоль оси , а его модуль равен сумме модулей складываемых векторов:

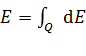, (2)

где напряженность поля 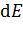, создаваемого точечным зарядом 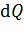, который находится на участке бесконечно малой длиной 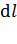, определяется формулой

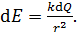(3)

Здесь величина заряда 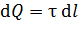, где 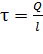– линейная плотность заряда нити; – расстояние от заряда 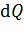до исследуемой точки поля .

Подставим формулу (3) в уравнение принципа суперпозиции (2), заменяя элемент длины участка нити 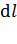равной ему величиной 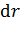, – бесконечно малым приращением переменной . Определим пределы интегрирования по этой переменной. В уравнении (2) суммируются поля напряженностью 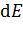всех элементарных зарядов нити 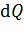, начиная с расположенного на расстоянии 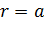от точки поля и заканчивая зарядом, находящимся на другом конце нити, – на расстоянии 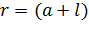от исследуемой точки. Проинтегрируем в указанных пределах:

;

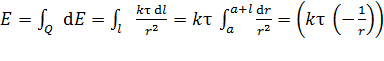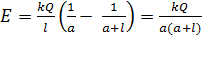. (4)

Проверим полученную расчетную формулу путем экстраполяции зависимости (4): увеличим расстояние от конца нити до точки так, чтобы 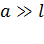; при этом условии заряженную нить можно принять за точечный заряд, а в формуле (4) полагать расстояние 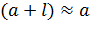, вследствие малости второго слагаемого. Таким образом, из формулы (4) получаем величину 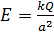, равную напряженности поля, создаваемого точечным зарядом 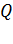в точке поля, находящейся на расстоянии от заряда. Следовательно, полученная формула (4) верна.

Вычисляем напряженность поля нити в точке по формуле (4):

.

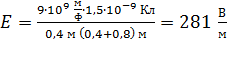2) Рассчитаем потенциал 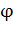электростатического поля в точке , используя принцип суперпозиции: суммируя бесконечно малые величины потенциала 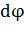полей, создаваемых элементарными зарядами :

;

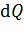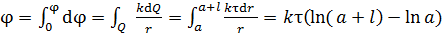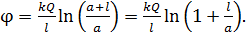(5)

Полученную формулу (5) также проверим на предельный случай точечного заряда: нить на расстоянии 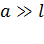; при этом используем формулу приближенных вычислений 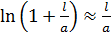, так как 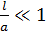. Подставляя это значение логарифма в выражение (5) получаем формулу в виде 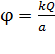– как для потенциала поля, созданного точечным зарядом 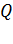. Следовательно, полученная формула (5) верна.

Вычисляем по формуле (5) потенциал поля в заданной точке :

.

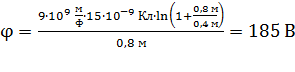Задача 8.Электростатическое поле создается нитью длиной 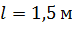, с зарядом 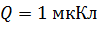, равномерно распределенным по длине. Определите напряженность 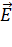и потенциал 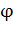поляв точке (рис. 17), находящейся на расстоянии 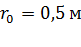от нити и равноудаленной от ее концов.

Дано Решение

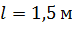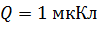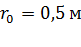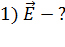; ; . 2)

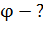
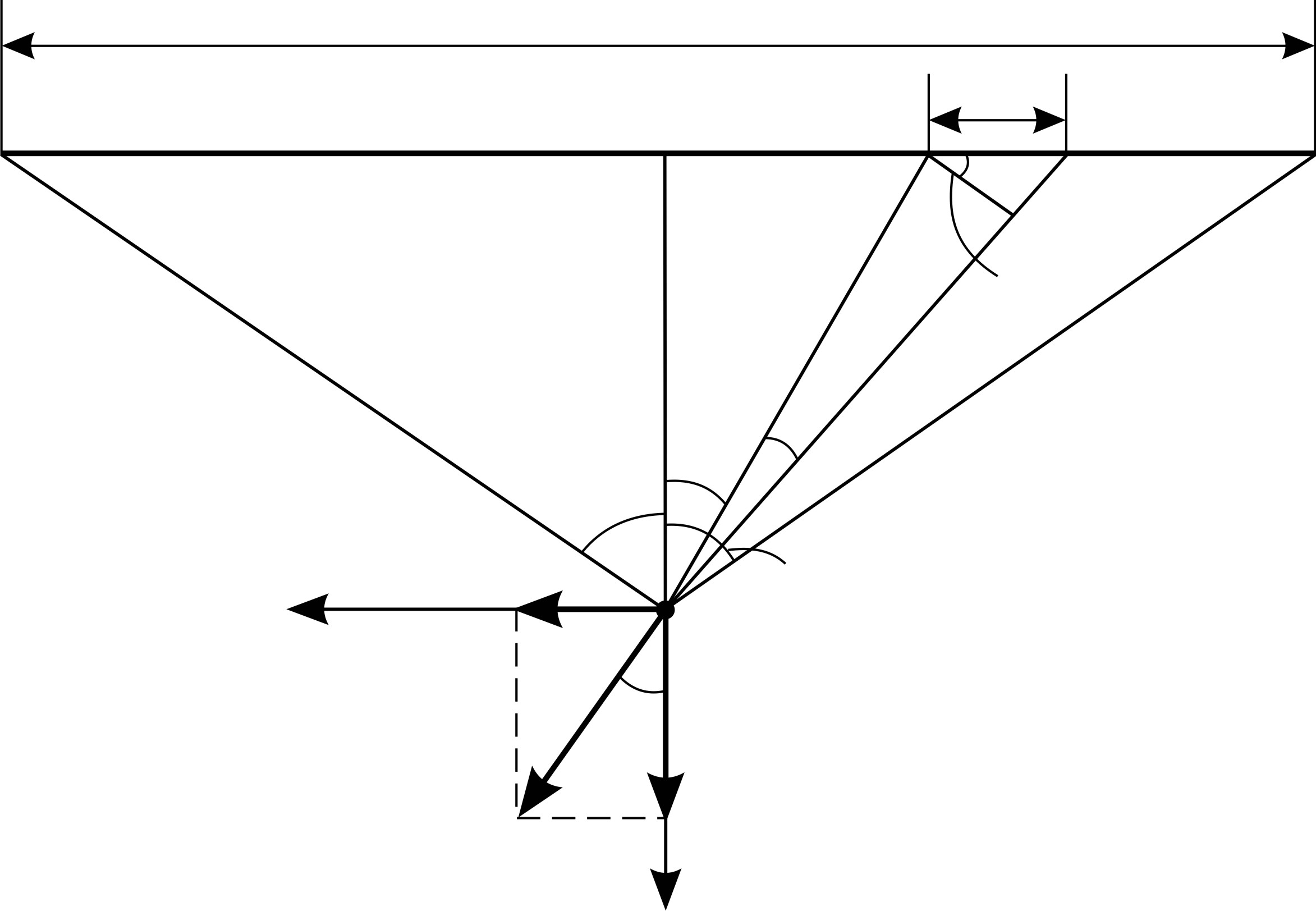
1) Заряд 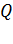, находящийся на нити, не является точечным, так как расстояние от заряда до точки
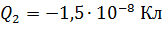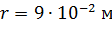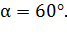
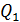
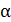
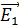
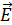
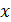
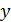
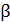
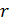
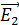
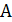
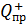
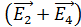
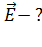
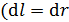