Дискретные случайные величины
Определение 1.Если случайная величина принимает конечное или счётное число значений 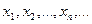 , то случайная величина называется дискретной (обозначение ДСВ).
, то случайная величина называется дискретной (обозначение ДСВ).
Закон распределения дискретной случайной величины ξ определяется значениями 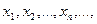 которые принимает ξ и вероятностями
которые принимает ξ и вероятностями 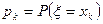 этих значений. Закон распределения можно определить с помощью таблицы, верхний ряд которой состоит из различных чисел хi , а числа нижнего ряда из чисел pi
этих значений. Закон распределения можно определить с помощью таблицы, верхний ряд которой состоит из различных чисел хi , а числа нижнего ряда из чисел pi
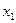
| 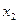
| … | 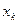
| … |
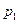
| 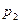
| … | 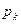
| … |
Таблица (а значит закон распределения) служит исчерпывающей характеристикой ДСВ, поскольку по этой таблице однозначно восстанавливается функция распределения F(x) ДСВ ξ.
Остается ещё добавить, что
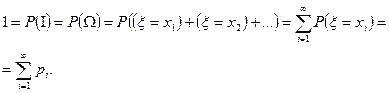
Итак
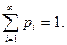 (1)
(1)
Выясним, какой вид имеет функция распределения ДСВ.
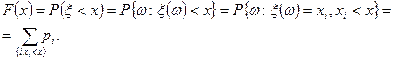 Итак
Итак
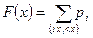 . (2)
. (2)
На рисунке 1 изображен график этой функции для частного случая, когда ξ принимает только три значения 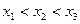
Если 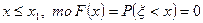 .
.
Если 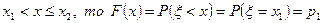 .
.
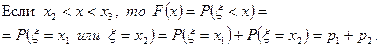
Если 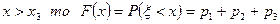 .
.
График представляет собой ступенчатую ломаную со скачками в точках 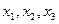 . Величины скачков равны соответственно
. Величины скачков равны соответственно 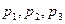 . Аналогичная ступенчатая ломаная будет получаться для любой ДСВ ξ.
. Аналогичная ступенчатая ломаная будет получаться для любой ДСВ ξ.
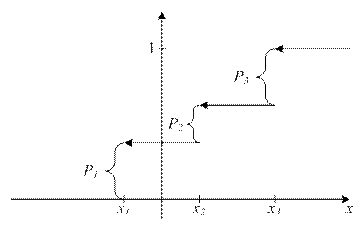 Рис. 1
Рис. 1
Примеры законов распределения ДСВ:
1. Биномиальный закон для числа успехов ξ при n независимых испытаниях в схеме Бернулли:
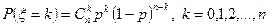 .
.
2. Гипергеометрическое распределение числа белых шаров ξ в выборке без возвращения объема n из урны, содержащей m белых и N- m черных шаров (см.§1)
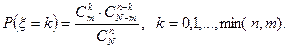
3. Равномерное распределение на множестве 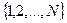
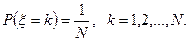
4. Пуассоновское распределение числа вызовов ξ на телефонную станцию, поступающих за единицу времени, если λ есть среднее число вызовов, поступающих за единицу времени
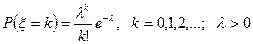 .
.
5. Геометрическое распределение. Производится ряд независимых опытов, в каждом из которых с одной и той же вероятностью p наступает событие А. Опыты продолжаются до первого появления события А, после чего прекращаются. Случайная величина ξ – число произведённых опытов, распределена по геометрическому закону
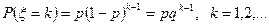 .
.
Дата добавления: 2021-01-11; просмотров: 528;











