Системы случайных величин.

В практических задачах часто встречается ситуации, при которых те или иные случайные величины приходится изучать совместно.

Систему из двух случайных величин 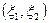можно истолковать как случайную точку на плоскости, систему трёх случайных величин 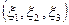– как случайную точку в трехмерном пространстве и т.д.

Ограничимся двумерным случаем; обобщение на любое число случайных величин не представляет особых затруднений.

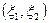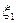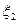Понятие системы двух случайных величин связано с представлением об опыте, результатом которого является пара чисел . Поскольку исход опыта есть случайное событие, то предсказать значения чисел и невозможно (при повторении опыта они меняются непредвиденным образом). Приведём примеры.

Пример 1. Дважды бросается игральная кость. Обозначим через 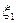, число очков при первом бросании, через 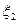– число очков при втором. Пара 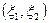будет системой двух случайных величин или двумерной случайной величиной.

Пример 2. Из некоторой аудитории наугад выбирается один человек; 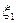-его рост (пусть в сантиметрах), 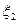- вес (в килограммах).

Пример 3. Сравниваются письменные работы по математике и физике: 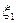- оценка за работу по математике, 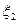- оценка за работу по физике.

Пример 4. Рассмотрим квартиры в многоэтажном доме, в которых есть семья (муж и жена). Выберем наудачу некоторую семью и обозначим через 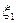- возраст мужа,

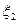– возраст жены, выраженные в целых числах лет. Возможные значения 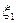, 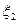здесь можно считать целыми числами от 16 до 100.

Поскольку с каждым опытом связано некоторое вероятностное пространство (вероятностная схема см. § 5. гл.1) (Ω, S, P) , то рассмотрим на нём две случайные величины 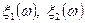, где 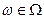(в общем случае рассматривается n случайных величин). Так как множества 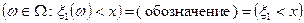и 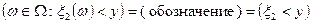принадлежат S, т.е. являются событиями, то и их пересечение (или, что

то же самое, произведение) 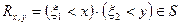. Поэтому существует вероятность этого события, которая называется двумерной функцией распределения.

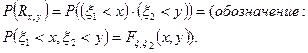(1)

В дальнейшем эту двумерную функцию распределения мы будем иногда записывать просто 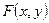не указывая индексы , .

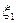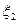Системы случайных величин, чаще всего встречающиеся в приложениях, подразделяются на два типа: дискретные и непрерывные.