Расчет показателей надежности невосстанавливаемых резервированных систем

В резервированной системе отказ какого-либо элемента не обязательно приводит к отказу всей системы. Типичным случаем является логически параллельное соединение элементов (рис.5), при котором система отказывает тогда, когда отказывают все ее элементы. Такой тип резервирования называют постоянным или нагруженным m-кратным резервированием. В этом случае все элементы выполняют одну и ту же функцию, работают одновременно и равнонадежны. По теореме умножения вероятностей имеют место следующие выражения:

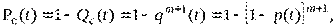
где q(t), p(t) – соответственно вероятности отказа и безотказной работы одного элемента.

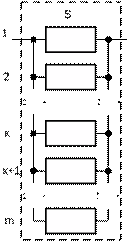
Рисунок. 5. Схема логического соединения элементов резервированной системы

Если для элементов справедлив экспоненциальный закон распределения надежности, то

.

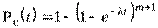Для высоконадежных систем, у которых lt<0,1 и 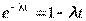, имеем

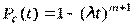
Среднее время наработки до отказа резервированной системы:

,

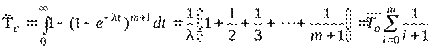где 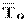- среднее время наработки до отказа основной системы или любой из резервных систем.

Кроме m-кратного резервирования (m целое число) используют также резервирование с дробной кратностью, которое называют логическим соединением «k из n». Это означает, что система работоспособна, если работоспособны не менее k элементов. На рис.5,б приведена структурная схема «k из n» с кратностью резервирования m = .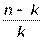

Универсальным методом расчета надежности любой резервированной системы со сложной логической структурой является метод полной группы событий. В момент времени t состояние системы S может быть задано двоичным вектором A(t) = 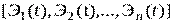, где Э_i(t)=1, если в момент t i-й элемент работоспособен, и Э_i(t)=0, если к этому моменту он уже отказал. Всего существует 2ⁿ состояний, которые образуют полную группу событий. Пусть надо рассчитать вероятность безотказной работы P(t) системы «2 из 3». Все возможные состояния этой системы приведены в табл.3.1

Таблица 3.1