Раздельное резервирование замещением с дробной кратностью
Этот вид резервирования (рис.9,е) применяется, если все элементы системы выполняют одинаковые функции. Основная система имеет nэлементов, а m элементов находятся в холодном резерве. При отказе любого работающего элемента на его место подключается любой из резервных. Кратность резервирования 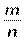 . Предположим, что все элементы равнонадежны с l = const и переключающие устройства абсолютно надежны.
. Предположим, что все элементы равнонадежны с l = const и переключающие устройства абсолютно надежны.
Система будет работоспособна, если за время t произойдут следующие несовместимые события: А0 – система не имеет отказов; А1 – отказал один элемент; Аm – отказали m элементов. Вероятность событий Аi(i = 0, 1, …m) определяется по закону Пуассона, поэтому величина Pc(t) рассчитывается по формуле

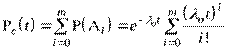 .
.
Это означает, что надежность данной системы равна надежности системы с общим резервированием с замещением, но в то же время имеет в n раз меньше резервных элементов. Однако переключающие устройства при этом усложняются.
Типовые примеры
Пример 1. Схема расчета надежности устройства приведена на рисунке:
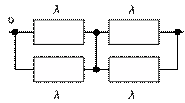
Предполагается, что последствие отказов отсутствует и все элементы расчета равнонадежны. Интенсивность отказа элементов 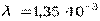 1/ч. Требуется определить наработку до первого отказа резервированной системы.
1/ч. Требуется определить наработку до первого отказа резервированной системы.
Решение. В данном случае имеет место раздельное резервирование равнонадежных устройств с постоянно включенным резервом. Число элементов нерезервированной системы n=2, кратность резервирования m=1. Для вычисления средней наработки до первого отказа воспользуемся формулой:
. 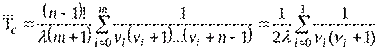 .
.
Так как
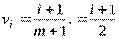 ,
,
то 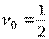 ,
, 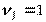 .
.
Тогда
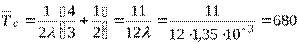 (ч)
(ч)
.Пример 2. Вероятность безотказной работы преобразователя постоянного тока в переменный в течение t=1000 ч равна 0,95. Для повышения надежности системы электроснабжения на объекте имеется такой же преобразователь, который включается в работу при отказе первого. Требуется рассчитать вероятность безотказной работы и среднюю наработку до первого отказа системы, состоящей из двух преобразователей.
Решение. В данном случае имеет место общее резервирование замещением кратности m=1. Для расчета вероятности безотказной работы воспользуемся формулой:
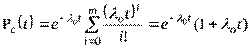 .
.
По условию задачи вероятность безотказной работы основной системы 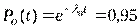 , тогда
, тогда 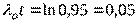 . Подставив эти значения в формулу, получим:
. Подставив эти значения в формулу, получим:
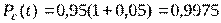 .
.
Среднюю наработку до первого отказа системы рассчитаем по формуле:
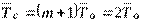 .
.
Так как в течение времени t=1000 ч 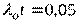 , то
, то 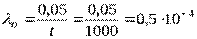 (1/ч), а средняя наработка до первого отказа нерезервированного преобразователя
(1/ч), а средняя наработка до первого отказа нерезервированного преобразователя 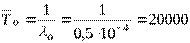 (ч).
(ч).
Тогда средняя наработка до первого отказа резервированной системы
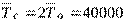 (ч).
(ч).
Пример 3. Система имеет кратность общего резервирования m=5. Основная нерезервированная система содержит четыре равнонадежных элемента с логически последовательным соединением. Интенсивность отказа одного элемента 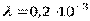 (1/ч). Определить характеристики надежности системы за 1000 ч.
(1/ч). Определить характеристики надежности системы за 1000 ч.
Решение. Определим интенсивность отказов основной системы по формуле
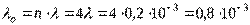 (1/ч).
(1/ч).
Вероятность безотказной работы системы определим по формуле
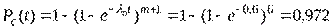 .
.
Среднее время наработки на отказ и интенсивность отказов системы соответственно равны
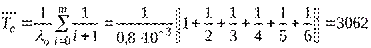 (ч).
(ч).
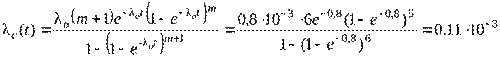
Пример 4. Вычислительная система построена из 500 однотипных блоков с интенсивностью отказа 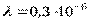 1/ч. В скользящем холодном резерве находятся пять таких же блоков, которые могут заменить любой из отказавших блоков. Определить показатели надежности системы за 10000 часов.
1/ч. В скользящем холодном резерве находятся пять таких же блоков, которые могут заменить любой из отказавших блоков. Определить показатели надежности системы за 10000 часов.
Решение. Определим показатели надежности системы, используя формулы
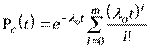
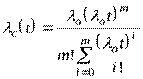
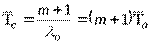
Определим интенсивность отказов основной системы за время t=10000 ч 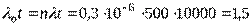 . Тогда
. Тогда
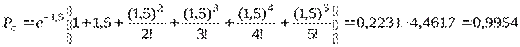
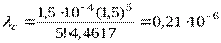 (1/ч)
(1/ч)
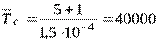 (ч).
(ч).
Дата добавления: 2016-10-07; просмотров: 5199;











