Расчет показателей надежности

Расчет показателей надежности невосстанавливаемых нерезервированных систем

В качестве объекта, надежность которого требуется определить, рассмотрим некоторую сложную систему S, состоящую из отдельных элементов (блоков). Задача расчета надежности сложной системы состоит в том, чтобы определить ее показатели надежности, если известны показатели надежности отдельных элементов и структура системы, т.е. характер связей между элементами с точки зрения надежности.

Наиболее простую структуру имеет нерезервированная система, состоящая из n элементов, у которой отказ одного из элементов приводит к отказу всей системы. В этом случае система S имеет логически последовательное соединение элементов (рис.4).

Рисунок 4. Схема логического соединения элементов нерезервированной системы

Методы расчета

В зависимости от полноты учета факторов, влияющих на работу изделия, различают ориентировочный и полный расчет показателей надежности.

При ориентировочном расчете показателей надежности необходимо знать структуру системы, номенклатуру применяемых элементов и их количество. Ориентировочный расчет учитывает влияние на надежность только количества и типов, входящих в систему элементов, и основывается на следующих допущениях:

- все элементы данного типа равнонадежны, т.е. величины интенсивности отказов ( 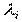) для этих элементов одинаковы;

- все элементы работают в номинальном (нормальном) режиме, предусмотренном техническими условиями;

- интенсивности отказов всех элементов не зависят от времени, т.е. в течение срока службы у элементов, входящих в изделие, отсутствует старение и износ, следовательно ;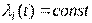

- отказы элементов изделия являются событиями случайными и независимыми;

- все элементы изделия работают одновременно.

Ориентировочный метод расчета используется на этапе эскизного проектирования после разработки принципиальных электрических схем изделий и позволяет наметить пути повышения надежности изделия.

Пусть отказы элементов есть независимые друг от друга события. Так как система работоспособна, если работоспособны все ее элементы, то согласно теореме об умножении вероятностей вероятность безотказной работы системы Р_с (t) равна произведению вероятностей безотказной работы ее элементов:

,

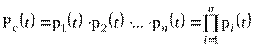где 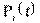- вероятность безотказной работы i-го элемента.

Пусть для элементов справедлив экспоненциальный закон распределения надежности и известны их интенсивности отказов. Тогда и для системы справедлив экспоненциальный закон распределения надежности:

,

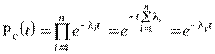где 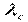- интенсивность отказов системы.

Интенсивность отказов нерезервированной системы равна сумме интенсивностей отказов ее элементов:

.

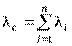Если все элементы данного типа равнонадежны, то интенсивность отказов системы будет

,

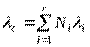где: 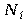- число элементов i-го типа; r – число типов элементов.

Выбор 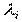для каждого типа элементов производится по соответствующим таблицам.

Среднее время наработки до отказа и частота отказов системы соответственно равны:

, .

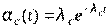На практике очень часто приходится вычислять вероятность безотказной работы высоконадежных систем. При этом произведение 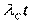значительно меньше единицы, а вероятность безотказной работы P(t) близка к единице. В этом случае количественные характеристики надежности можно с достаточной для практики точностью вычислить по следующим приближенным формулам:

, , , .

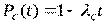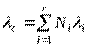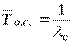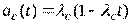При расчете надежности систем часто приходится перемножать вероятности безотказной работы отдельных элементов расчета и возводить их в степень. При значениях вероятность P(t), близких к единице, эти вычисления можно с достаточной для практики точностью выполнить по следующим приближенным формулам:

, ,

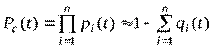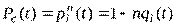где 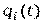- вероятность отказа i-го блока.

Полный расчет показателей надежности изделия выполняется тогда, когда известны реальные режимы работы элементов после испытания в лабораторных условиях макетов изделия.

Элементы изделия находятся обычно в различных режимах работы, сильно отличающихся от номинальной величины. Это влияет на надежность как изделия в целом, так и отдельных его составляющих частей. Выполнение окончательного расчета параметров надежности возможно только при наличии данных о коэффициентах нагрузки отдельных элементов и при наличии графиков зависимости интенсивности отказов элементов от их электрической нагрузки, температуры окружающей среды и других факторов, т.е. для окончательного расчета необходимо знать зависимости

.

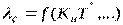Эти зависимости приводятся в виде графиков либо их можно рассчитать с помощью так называемых поправочных коэффициентов интенсивности отказов .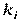

При разработке и изготовлении элементов обычно предусматриваются определенные, так называемые «нормальные» условия работы. Интенсивность отказов элементов в «нормальном» режиме эксплуатации называется номинальной интенсивностью отказов .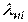

Интенсивность отказов элементов при эксплуатации в реальных условиях 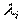равна номинальной интенсивности отказов 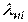, умноженной на поправочные коэффициенты 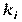, т.е.

,

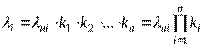где: 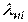- интенсивность отказов элемента, работающего в нормальных условиях при номинальной электрической нагрузке; 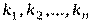- поправочные коэффициенты, зависящие от различных воздействующих факторов.

Полный расчет надежности применяется на этапе технического проектирования изделия.

Типовые примеры

Пример 1. Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t = 100 ч. равны: р₁(100) = 0,95; р₂ (100) = 0,97. Справедлив экспоненциальный закон распределения надежности. Необходимо найти среднюю наработку до первого отказа системы.

Решение. Найдем вероятность безотказной работы системы по формуле:

.

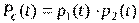Отсюда .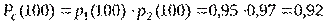

Найдем интенсивность отказов системы. Для этого воспользуемся формулой:

.

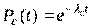Тогда 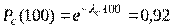. Из этого выражения найдем .

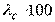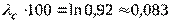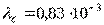или (1/ч).

Среднее время наработки до первого отказа

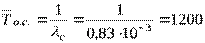(ч).

Пример 2. В системах могут быть использованы только элементы, интенсивность отказов которых равна 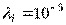1/ч. Системы имеют число элементов N₁ = 500, N₂ = 2500. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа P_c(t)

Решение. Определим интенсивность отказов систем

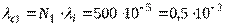(1/ч).

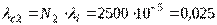(1/ч).

Тогда

,

.

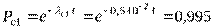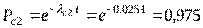Среднее время наработки до первого отказа

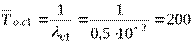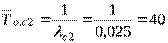(ч).

(ч).

Пример 3. Система состоит из пяти приборов, вероятность исправной работы которых в течение времени t = 100 ч равны: 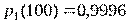; ; 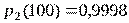; ; 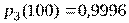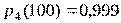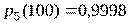. Требуется определить частоту отказов системы в момент времени t = 100.

Предполагается, что отказы приборов независимы и для них справедлив экспоненциальный закон распределения надежности.

Решение. Вероятность безотказной работы системы

.

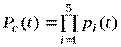Так как система является высоконадежной (вероятности безотказной работы близки к единице), то вероятность безотказной работы системы можно вычислить по формуле

.

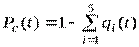Определим вероятность отказа каждого блока:

,

,

, :,

:.

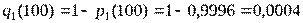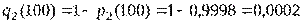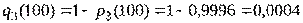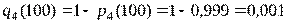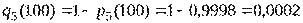Тогда

.

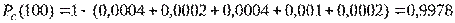Интенсивность отказов системы найдем из выражения

,

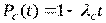отсюда

.

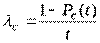Подставляя значения P_c(100) и время t =100 ч, получим

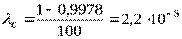(1/ч).

Частота отказов

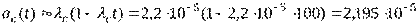(1/ч).