Умножение матриц ленточным методом

Из определения операции матричного умножения следует, что вычисление всех элементов матрицы С может быть выполнено независимо друг от друга. Как результат, возможный подход для организации параллельных вычислений состоит в использовании в качестве базовой подзадачи процедуры определения одного элемента результирующей матрицы С. Для проведения всех необходимых вычислений каждая подзадача должна содержать по одной строке матрицы А и одному столбцу матрицы В. Общее количество получаемых при таком подходе подзадач оказывается равным 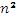(по числу элементов матрицы С). Можно отметить, что достигнутый уровень параллелизма является в большинстве случаев избыточным. Обычно при проведении практических расчетов такое количество сформированных подзадач превышает число имеющихся процессоров и делает неизбежным этап укрупнения базовых задач. Поэтому определим базовую задачу как процедуру вычисления всех элементов одной из строк матрицы С. Такой подход приводит к снижению общего количества подзадач до величины n. Для выполнения всех необходимых вычислений базовой подзадаче должны быть доступны одна из строк матрицы A и все столбцы матрицы B. Простое решение этой проблемы – дублирование матрицы B во всех подзадачах не является оптимальным с точки зрения затрат памяти на хранение данных. Поэтому организация вычислений должна быть построена таким образом, чтобы в каждый текущий момент времени подзадачи содержали лишь часть данных, необходимых для проведения расчетов, а доступ к остальной части данных обеспечивался бы при помощи передачи данных между процессорами.

Алгоритм представляет собой итерационную процедуру, количество итераций которой совпадает с числом подзадач. На каждой итерации алгоритма каждая подзадача содержит по одной строке матрицы А и одному столбцу матрицы В. При выполнении итерации проводится скалярное умножение содержащихся в подзадачах строк и столбцов, что приводит к получению соответствующих элементов результирующей матрицы С. По завершении вычислений в конце каждой итерации столбцы матрицы В должны быть переданы между подзадачами с тем, чтобы в каждой подзадаче оказались новые столбцы матрицы В и могли быть вычислены новые элементы матрицы C. При этом данная передача столбцов между подзадачами должна быть организована таким образом, чтобы после завершения итераций алгоритма в каждой подзадаче последовательно оказались все столбцы матрицы В. Возможная простая схема организации необходимой последовательности передач столбцов матрицы В между подзадачами состоит в представлении топологии информационных связей подзадач в виде кольцевой структуры. В этом случае на каждой итерации подзадача i, 0i<n, будет передавать свой столбец матрицы В подзадаче с номером i+1 (в соответствии с кольцевой структурой подзадача n-1 передает свои данные подзадаче с номером 0).

Когда размер матриц n оказывается больше, чем число процессоров p, базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько соседних строк и столбцов перемножаемых матриц. Размер полос при этом следует выбрать равным k=n/p (мы считаем, что n кратно p).