Алгоритмы параллельного поиска и сортировки
Параллельный поиск минимального элемента в массиве – достаточно легкая задача, во многом аналогичная задачам из первой лабораторной работы. Исходный массив 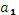 ,
, 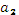 , .. ,
, .. , 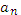 , состоящий из n элементов, и находящийся во входном файле, нужно распределить по m процессорам, используя функции MPI_Scatter или MPI_Scatterv. Отличие MPI_Scatterv от MPI_Scatter в том, что при помощи нее можно разделять массивы произвольной длины, т.е. разер массива не должен обязательно делиться нацело на число процессоров. При этом чтение массива из файла осуществляет только корневой процесс, далее каждый процесс узнает длину своей части массива, выделяет под нее память при помощи malloc и получает свой локальный массив. Далее каждый процесс ведет поиск своего локального минимума, следом за этим корневой процесс опять собирает все локальные минимумы при помощи редукционной операции MPI_Reduce с опцией MPI_MIN. Аналогочно решается задача поиска максимального элемента или суммы элементов массива.
, состоящий из n элементов, и находящийся во входном файле, нужно распределить по m процессорам, используя функции MPI_Scatter или MPI_Scatterv. Отличие MPI_Scatterv от MPI_Scatter в том, что при помощи нее можно разделять массивы произвольной длины, т.е. разер массива не должен обязательно делиться нацело на число процессоров. При этом чтение массива из файла осуществляет только корневой процесс, далее каждый процесс узнает длину своей части массива, выделяет под нее память при помощи malloc и получает свой локальный массив. Далее каждый процесс ведет поиск своего локального минимума, следом за этим корневой процесс опять собирает все локальные минимумы при помощи редукционной операции MPI_Reduce с опцией MPI_MIN. Аналогочно решается задача поиска максимального элемента или суммы элементов массива.
Задача поворота трехмерной фигуры в пространстве вокруг одной из осей координат также легко решается при помощи функций коллективного взаимодействия MPI. Корневой процесс выделяет память под массив, читает его из входного файла, затем делит его между остальными процессами при помощи MPI_Scatter или MPI_Scatterv. Каждый процесс также выделяет память под свою часть массива и производит над ней необходимую операцию – поворот вокруг оси. По окончании поворота все процессы вызывают MPI_Gather и передают результаты вычислений корневому процессу. При этом на узлах расходуется памяти под массив меньше, чем в корневом процессе в m+1 раз (m-число процессов).
С алгоритмами сортировки массивов все намного сложнее. Сортировке данных посвящена обширная литература. Монография Кнута [1]
содержит подробное описание и анализ огромного количества различных алгоритмов. Рассматривамый далее параллельный алгоритм предполагает двухэтапную сортировку:
- последовательную сортировку фрагментов массива, распределенных по
процессорам системы;
- объединение упорядоченных фрагментов массива – перемещение элементов
массива между процессорами.
Время сортировки массива зависит от множества факторов, среди которых не
последнее место занимает характер распределения чисел в сортируемом массиве (степень его упорядоченности перед началом сортировки). В качестве тестовых данных используются различные массивы целых четырехбайтовых чисел:
- псевдослучайные неупорядоченные числа;
- числа, расположенные по не возрастанию;
- числа, расположенные по не убыванию.
Далее приняты следующие обозначения:
n - число элементов в сортируемом массиве;
p - число процессоров;
T(n, p) - общее время сортировки массива из n элементов на p процессорах;
M(n, p) - общее число условных операций, необходимых для сортировки
массива из n элементов на p процессорах.
Подробное описание алгоритмов быстрой, пирамидальной и «обменной
сортировки со слиянием» Бэтчера, четно-нечетного слияния, а также сортировки слиянием списков можно найти в монографии [1], там же приведен анализ соответствующих алгоритмов, необходимые доказательства и оценка объема выполняемых алгоритмами действий.
| Алгоритм Сортировки | Среднее время |
| Быстрая (qsort) | 11.7 n log2n [1] |
| Пирамидальная (hsort) | 16 n log2n [1] |
| Слияние списков (lsort) | 10 n log2n [1] |
| Параллельная сортировка сдваиванием | 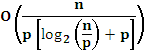
|
| Параллельная «обменная сортировка со слиянием» | 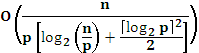
|
Будем предполагать, что p используемых процессоров имеют номера от 0 до p-1. Будем предполагать, что в начале исходный массив распределен по процессорам некоторыми порциями 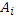 , где i –номер процессора. По окончании сортировки элементы исходного массива распределены по процессорам некоторыми упорядоченными по не убыванию порциями
, где i –номер процессора. По окончании сортировки элементы исходного массива распределены по процессорам некоторыми упорядоченными по не убыванию порциями 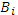 .
.
Для простоты изложения будем также предполагать, что p=2r, где r –
натуральное число. Рассмотрим параллельных алгоритма сортировки массивов на основе метода сдваивания.
Параллельный алгоритм сортировки массива на основе метода сдваивания
состоит из двух этапов:
1) на каждом из процессоров с помощью алгоритма пирамидальной сортировки сортируется фрагмент массива i A длинной pA n i = . При этом, для простоты анализа, будем предполагать, что n=vp, где v - целое неотрицательное число.
2) элементы отсортированных на первом этапе фрагментов i A
упорядочиваются с помощью слияния, причем последовательность слияний
определяется методом сдваивания (Рис. 3).
Задание
В соответствии с вариантом задания написать программу реализации параллельного алгоритма. Запустить программу на узле, затем на сервере с небольшим объемом входных данных и убедиться, что она работает. После проверки запустить программу на сгенерированном случайным образом объеме входных данных, указанном в варианте, замерить время выполнения на одном процессоре, затем на числе процессоров, указанном в варианте.
· Изучить программу генерации файла с исходным массивом данных.
Варианты
| Номер варианта | Задача | Объем входных данных | Число процессоров |
| 1* | Сортировка массива | 1 Mb | |
| Поворот фигуры в пространстве | 10 Mb | ||
| Поиск минимального элемента массива | 20 Mb | ||
| 4* | Сортировка массива | 2 Mb | |
| Поворот фигуры в пространстве | 20 Mb | ||
| Поиск максимального элемента массива | 30 Mb | ||
| 7* | Сортировка массива | 4 Mb | |
| Поворот фигуры в пространстве | 4 Mb | ||
| Поиск суммы элементов массива | 1 Mb | ||
| 10* | Сортировка массива | 3 Mb | |
| Поворот фигуры в пространстве | 20 Mb | ||
| Поиск среднего арифметического элементов массива | 6 Mb | ||
| 13* | Сортировка массива | 4 Mb | |
| Поворот фигуры в пространстве | 10 Mb | ||
| Поиск числа нулевых элементов массива | 40 Mb | ||
| 16* | Сортировка массива | 1 Mb | |
| Поворот фигуры в пространстве | 5 Mb | ||
| Поиск минимального элемента массива | 10 Mb | ||
| 19* | Сортировка массива | 10 Mb | |
| Поворот фигуры в пространстве | 12 Mb |
Содержание отчета
· Описать алгоритм задачи согласно предложенному варианту.
· Подготовка исходных данных в файле.
· Текст параллельной программы на языке С.
· Результаты запуска программы на одном узле, время выполнения, результат работы.
· Результаты запуска программы на нескольких узлах, время выполнения, результат работы .
· Рекомендации по улучшению быстродействия программы, выводы.
Дата добавления: 2016-05-31; просмотров: 3134;











