Движение тела под действием силы тяготения

Если рассматривать движение планет или других тел (астероидов, комет) вокруг Солнца, то в большинстве случаев влиянием других тел («в первом приближении») можно пренебречь. В таком случае мы имеем дело с задачей двух тел. Математически строго эта задача решается путем интегрирования дифференциальных уравнений движения, получаемых из основного уравнения динамики материальной точки (4.14), в котором сила F есть сила тяготения. Это решение подробно рассматривается в курсах небесной механики или космической геодезии. Мы же получим основные выводы более простым путём.

Будем считать, что массы обоих тел сосредоточены в их центрах и следовательно их поле тяготения будет центральным или сферическим.

Пусть меньшее тело с масса m двигаясь в поле тяготения притягивающего тела с массой M имело в начальный момент скорость V₀ на расстоянии от r₀ от тела М (V₀ и r₀ ¾ начальные условия).

В дальнейшем используем закон сохранения энергии, который гласит, что

для изолированной физической системы энергия сохраняется с течением времени.

Кинетическая энергия тела m равна

E_k=mV²/2, (4.21)

потенциальная энергия в центральном поле тяготения выражается формулой

E_p=- fMm/r. (4.22)

Закон сохранения полной механической энергии для тела массой m, двигающегося в поле тяготения другого тела массой М запишется в следующем виде:

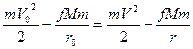. (4.23)

В формуле (4.23) в левой части равенства стоит сумма кинетической и потенциальной энергий в начальный момент, а в правой ¾ в любой другой момент времени. После сокращения на m и преобразований, мы получим интеграл энергии :

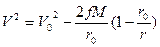, (4.24)

Если заменить fM=K , то К ¾ гравитационный параметр, зависящий от массы притягивающего тела, который для Солнца равен К=1,3272×10¹¹ км³/сек², то (4.25) можно записать

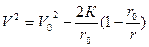. (4.25)