Прецессия и нутация
Греческий астроном Гиппарх (123 г. до н.э.) определяя координаты звёзд и сравнивая их с аналогичными наблюдениями Аристилла и Тимохариса, произведенными на 100 лет раньше нашел, что широты звезд остались неизмененными, а склонения заметно изменились. Это указывало на смещение экватора относительно эклиптики и следовательно смещение точки весеннего равноденствия (ТВР, ^) навстречу движения Солнца по эклиптике. Явление это на латыни получило название прецессия, что можно перевести как предварение равноденствия. Причину этого явления объяснил Ньютон, после открытия им закона всемирного тяготения.
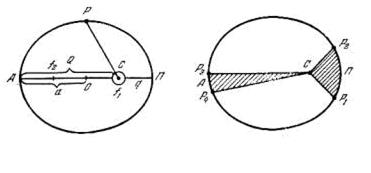
Земля не имеет точной сферической формы, а близка к сфероиду (см. пп 2.9). Притяжение же сфероида каким-либо материальным телом L (рис. 3.26а) складывается из притяжения F шара, выделенного внутри сфероида (эта сила приложена к центру сфероида), притяжения F1 ближайшей к телу L половины экваториального выступа и притяжения F2 другой, более далекой, половины экваториального выступа. Сила F1 больше силы F2 и поэтому притяжение тела L стремится повернуть ось вращения сфероида РNРS так, чтобы плоскость экватора сфероида совпала с направлением TL (на рис. 3.26а против часовой стрелки). Из механики известно, что ось вращения PNPS в этом случае будет перемещаться в направлении, перпендикулярном к плоскости, в которой лежат силы F1 и F2 . На экваториальные выступы сфероидальной Земли действуют силы притяжения от Луны и от Солнца. В результате ось вращения Земли совершает очень сложное движение в пространстве. Прежде всего, она медленно описывает вокруг оси эклиптики конус, оставаясь все время наклоненной к плоскости движения Земли под углом около 66° 33' (рис. 3.26б ). Это движение земной оси называется прецессионным, период его около 26 000 лет. Вследствие прецессии земной оси полюсы мира за тот же период описывают вокруг полюсов эклиптики малые круги радиусом около 23° 27'. Прецессия, вызываемая действием Солнца и Луны, называется лунно-солнечной прецессией.
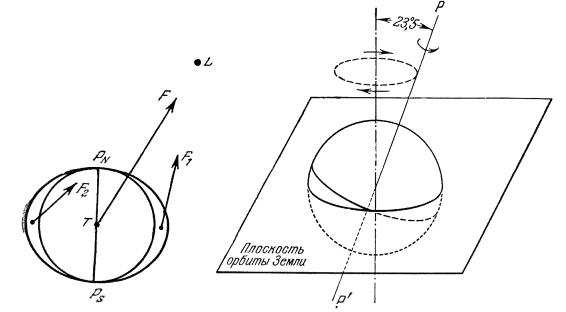
а) б)
Рис. 3.26
Кроме того, ось вращения Земли совершает различные мелкие колебания около своего среднего положения, которые называются нутацией земной оси.  Нутационные колебания возникают потому, что прецессионные силы Солнца и Луны (силы F1 и F2) непрерывно меняют свою величину и направление; они равны нулю, когда Солнце и Луна находятся в плоскости экватора Земли и достигают максимума при наибольшем удалении от него этих светил.
Нутационные колебания возникают потому, что прецессионные силы Солнца и Луны (силы F1 и F2) непрерывно меняют свою величину и направление; они равны нулю, когда Солнце и Луна находятся в плоскости экватора Земли и достигают максимума при наибольшем удалении от него этих светил.
Самое главное нутационное колебание земной оси имеет период в 18,6 года, равный периоду обращения лунных узлов (см. раздел 4.10). Вследствие этого движения земной оси полюсы мира описывают на небесной сфере эллипсы, большие оси которых равны 18²,42, а малые — 13'', 72.
Рис. 3.27
В результате прецессии и нутации земной оси полюсы мира в действительности описывают на небе сложные волнистые линии (рис. 3.27). Притяжение планет слишком мало, чтобы вызвать изменения в положении оси вращения Земли, но оно действует на движение Земли вокруг Солнца, изменяя положение в пространстве плоскости земной орбиты, т.е. плоскости эклиптики. Эти изменения положения плоскости эклиптики называются планетной прецессией, которая смещает точку весеннего равноденствия к востоку на 0²,114 в год.
Как уже было сказано, вследствие прецессионного движения земной оси полюсы мира за 26 000 лет описывают вокруг полюсов эклиптики круги радиусом приблизительно в 23°,5. Но так как полюсы эклиптики также перемещаются по небесной сфере (прецессия от планет), то кривые, описываемые полюсами мира, не замыкаются. На рис. 3.28 показано прецессионное движение северного полюса мира среди звезд.
 В настоящее время северный полюс мира находится вблизи звезды a Малой Медведицы, почему эта звезда и называется Полярной. Но 4000 лет назад ближе всех к северному полюсу мира была звезда a Дракона, а через 12 000 лет “полярной звездой” станет aЛиры (Вега).
В настоящее время северный полюс мира находится вблизи звезды a Малой Медведицы, почему эта звезда и называется Полярной. Но 4000 лет назад ближе всех к северному полюсу мира была звезда a Дракона, а через 12 000 лет “полярной звездой” станет aЛиры (Вега).
Вместе с изменением направления оси мира меняется и положение небесного экватора, плоскость которого перпендикулярна к этой оси и Рис.3.28
параллельна плоскости земного экватора. Плоскость эклиптики также несколько меняет свое положение в пространстве вследствие прецессии от планет. Поэтому точки пересечения небесного экватора с эклиптикой (точки равноденствий) медленно перемещаются среди звезд к западу. Скорость этого перемещения за год
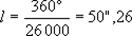
называется общей годовой прецессией в эклиптике. Общая годовая прецессия в экваторе m = 50",26 cose = 46²,11, где e — наклонение эклиптики к экватору, которое в настоящее время медленно уменьшается (на 0",47 в год), но через несколько тысяч лет уменьшение сменится столь же медленным увеличением, так как это возмущение (прецессия от планет) имеет периодический характер.
В начале нашей эры точка весеннего равноденствия находилась в созвездии Овна, а точка осеннего равноденствия — в созвездии Весов. Равноденственные точки обозначались тогда знаками этих созвездий ^ и d соответственно. С тех пор точка весеннего равноденствия переместилась в созвездие Рыб, а точка осеннего равноденствия — в созвездие Девы, но их обозначения остались прежними. Так как движение равноденственных точек направлено навстречу видимому годовому движению Солнца по эклиптике, то Солнце приходит в эти точки каждый раз несколько раньше, чем если бы они были неподвижными (слово «прецессия» и означает «предварение равноденствий»). По этой причине промежуток времени между последовательными прохождениями центра Солнца через точку весеннего равноденствия, называемый тропическим годом короче периода обращения Земли вокруг Солнца, называемого звездным годом. Разница между обоими годами составляет около 20 минут — столько времени нужно Солнцу, движущемуся по эклиптике к востоку со скоростью приблизительно 1° в сутки, чтобы пройти 51²,26.
Точка весеннего равноденствия является началом счета в. экваториальной и эклиптической системах координат. Поэтому вследствие ее движения к западу эклиптические долготы всех звезд ежегодно увеличиваются на 50",26, а эклиптические широты не изменяются, так как лунно-солнечная прецессия не изменяет положения плоскости эклиптики. Обе экваториальные координаты, прямое восхождение и склонение всех звезд непрерывно изменяются. В результате происходит медленное изменение вида звездного неба для данного места на Земле. Некоторые невидимые ранее звезды будут восходить и заходить, а некоторые видимые — станут невосходящими светилами. Так, например, через несколько тысяч лет в Европе можно будет наблюдать невидимый теперь Южный Крест, но зато нельзя будет увидеть Сириус и часть созвездия Ориона.
Литература к разделу
1. Волынский Б.А. Сферическая тригонометрия.-М.Наука,1977.
2. Плахов Ю.В., Краснорылов И.И. Геодезическая астрономия (часть 1 сферическая астрономия)
3. Халхунов В.З., Сферическая астрономия. М.: Недра,1972.
4. Куликовский П.Г. Справочник любителя астрономии/ Под ред. В.Г.Сурдина. Изд. 5-е, перераб. и полн. обновл.-М.: Эдиториал УРСС, 2002.-688с.
5. Астрономический календарь, постоянная часть/Под ред. В.К.Абалакина. Изд. 7-е, перераб.-Л.: Наука, 1981.-704с.
4. Строение и масштаб солнечной системы, движение планет.
Солнце и совокупность космических тел, обращающихся вокруг него, образуют Солнечную систему. Солнечной системой называется совокупность небесных тел, движущихся вокруг Солнца. В солнечную систему входят 8 больших планет вместо со спутниками, несколько малых планет (этот термин введён МАС в 2006 г. см. приложение , это Плутон, Квавар, Седна , Эрида, Церера), свыше 2300 малых планет (астероидов), десятки тысяч комет, бесчисленное множество метеоритных тел. Все эти тела объединены в одну систему благодаря силе притяжения центрального тела ¾ Солнца.
Тщательные научные исследования дали обширную информацию о движении этих тел в пространстве, что позволяет составить достаточно точный план строения Солнечной системы. В приложениях даны таблицы с числовыми характеристиками больших планет и их спутников — основных и наиболее массивных (после Солнца) членов Солнечной системы. Здесь же мы ограничимся лишь общим описанием ее строения.
Все планеты движутся вокруг Солнца в одном направлении, против часовой стрелки, если смотреть со стороны северного полюса эклиптики (прямое движение). Их невозмущенные орбиты — эллипсы, с небольшими эксцентриситетами и малыми наклонениями к эклиптике. Вращение почти всех больших планет, а также Солнца и Луны, вокруг осей происходит в том же направлении, в котором планеты движутся вокруг Солнца (прямое вращение). Исключением являются Уран и Венера (см. раздел 7.2), у которых вращение обратное. Расстояния планет от Солнца образуют закономерную последовательность: промежутки между орбитами увеличиваются с удалением от Солнца. Среднее расстояние от Солнца самой далекой планеты Плутон составляет 39,75 а.е. Если это расстояние принять за радиус Солнечной системы, то он окажется примерно в 700 раз меньше расстояния до ближайшей звезды Проксимы Центавра.
Спутники обращаются вокруг планет, подобно тому как планеты обращаются вокруг Солнца. Большинство спутников движется в прямом направлении, исключая 11 спутников с обратным движением, при этом 5 из них (спутники Урана) имеют, следовательно, то же направление движения, что и вращение планеты.
Закономерность расстояний планет от Солнца описывается эмпирической формулой (закон Тициуса-Боде):
an=0.4+0.3×2n ,(4.1)
где n - номер планеты, начиная с 0 для Венеры (для Меркурия n=-µ), в таблице- приведены рассчитанные по этой формуле и реальные расстояния от Солнца (см. таблицу 6). Из таблицы 5 видно, что средние расстояния планет вплоть до Урана удовлетворительно представляются формулой (4.1). Как раз в промежутке между Марсом и Юпитером, где должна была быть еще одна планета, находится пояс астероидов. По-видимому, в этой части Солнечной системы, которая разделяет планеты типа Земли и типа Юпитера, физические условия были таковы, что промежуточная планета не могла сформироваться или оказалась неустойчивой.
Таблица 6. Закон Тициуса-Боде
| Планета | Мерку-рий | Венера | Земля | Марс | Пояс астерои-дов | Юпитер | Сатурн | Уран | Нептун | Плутон |
| n | - ¥ | |||||||||
| An формула | 0,4 | 1,0 | 1,6 | 2,8 | 5,2 | 10,0 | 19,6 | 38,8 | 77,2 | |
| An реально | 0,39 | 0,72 | 1,00 | 1,52 | 2,68 | 5,2 | 9,55 | 19,19 | 30,07 | 39,52 |
Возможно, что на каком-то этапе эволюции Солнечной системы в поясе астероидов существовала одна или несколько крупных планет, но они были разрушены вследствие столкновений с другими телами или в результате действия какой-либо другой силы, например, приливного действия Юпитера. Физическая сущность приливного механизма разрушения состоит в том, что сила притяжения постороннего тела действует по-разному на различные части системы частиц, связанных между собой гравитацией, стремится их разделить и заставить каждую частицу двигаться по независимой орбите. Если это разделяющее действие окажется сильнее, чем притяжение между частицами, то система частиц (а ею может быть и твердое тело больших размеров, такое как планета) разрушится.
Малые планеты, или астероиды, движутся вокруг Солнца, как и большие планеты, в прямом направлении. Их орбиты имеют в среднем большие эксцентриситеты и большие наклоны, чем орбиты больших планет. Большинство орбит астероидов расположено между орбитами Марса и Юпитера, однако некоторые из них могут заходить внутрь орбиты Меркурия (Икар) и удаляться до орбиты Сатурна (Гидальго). У некоторых астероидов обнаружено вращение вокруг осей, причем в ряде случаев оно оказывается обратным.
Английский астроном К.Эджворс (1949 г.) и американский Дж. Койпер (1951 г.) на основании анализа орбит комет предположили существование пояса малых тел на расстоянии 35-50 а.е. от Солнца.
В 1992 г. за орбитой Нептуна был обнаружен объект диаметром 280 км, а к 2001 г. было открыто около 370 транснептунных объектов (http//www.ifa/hawaii.edu/faculty/jewitt/kb.html). Эти тела были отнесены к объектам пояса Эджвоса-Койпера. Среди них выделяется группа из нескольких десятков плутино ¾ объектов, большие полуоси которых как и у Плутона близки к 39,4 а.е..
Согласно современным представлением, солнечная система на расстоянии до 150 тыс. а.е. окружена роем кометных ядер (облако Орта), которые являются побочным продуктом при образовании планет солнечной системы. Многие ядра не приближаются к Солнцу, не образуют хвостов и не растрачивают своего вещества. Другие под влиянием окружающих Солнце звёзд меняют свои орбиты и, или навсегда покидают солнечную систему, или переходят на более короткопериодические орбиты и приближаются к солнцу. В этом случае мы можем наблюдать эти тела как кометы, имеющие хвост.
Движение комет отличается большим разнообразием. Невозмущенные орбиты большинства комет — очень сильно вытянутые эллипсы с эксцентриситетами, близкими к 1. В редких случаях, в результате возмущений от планеты, кометы вблизи Солнца движутся по гиперболам (е > 1), но те же возмущения могут возвратить кометы на эллиптические орбиты. Расстояние в афелии у некоторых комет достигает 50 000-100 000 а.е., а период обращения — нескольких миллионов лет. У немногих короткопериодических комет орбиты почти круговые. Наклонения орбит комет также разнообразны и часто превышают 90°, т.е. кометы движутся вокруг Солнца как в прямом, так и в обратном направлении. Движение отдельных метеорных тел очень сложное, но многие из них образуют метеорные потоки, движущиеся по орбитам, подобным орбитам комет. Более детально характеристики тел Солнечной системы будут рассмотрены в разделе 7.
4.1 Видимое движение планет, конфигурации планет
Все планеты движутся среди звёзд, но всегда остаются вблизи эклиптики. Их видимое движение ¾ сложная линия с зигзагами и петлями, которые были известны уже древним (см. рис. 4.1)

Рис. 4.1 Видимое движение Венеры в июле - декабре 2007 г. http://meteoweb.ru/astro/note009.php
Движение с запада на восток называется прямым движением, а с востока на запад ¾ попятным. Прямое движение планеты навстречу суточному движению небесной сферы (с запада на восток) сменяется кажущимся «стоянием» и затем понятным движением (с запада на восток), после чего вновь продолжается прямое движение. Дуга попятного движения меньше у планет, которые находятся дальше от Земли. Среднее значение дуг попятных движений у планет:
Меркурий – 12˚; Венера – 16˚; Марс – 15˚; Юпитер – 10˚; Сатурн – 7˚; Уран – 4˚; Нептун – 3˚; Плутон – 2˚.
По положению относительно Земли и Солнца все планеты делятся на нижние (внутренние) и верхние (внешние). К первым относятся Меркурий и Венера, а к верхним все остальные, начиная с Марса. Движение нижних (внутренних) планет отличается от верхних. Первые движутся вблизи Солнца, удаляясь от него максимально:
Меркурий на 28˚;
Венера на 48˚.
Наибольшее угловое удаление нижней планеты от Солнца называется элонгацией (западная и восточная). В западной элонгации планеты видны в конце ночи на востоке, в восточной элонгации на западе вечером. При восточной элонгации планета видна на западе в лучах вечерней зари (заход после Солнца), затем двигаясь попятно она скрывается в его лучах (нижние соединение) и затем появляется на востоке утром перед восходом Солнца. Двигаясь попятным движением, она удаляется от Солнца на максимальный угол (западная элонгация). После этого планета начинает прямое движение с запада на восток и опять приближается к Солнцу скрываясь за ним (верхние соединение), после чего появляется на западе вечером удаляясь от Солнца на максимум, т.е. планета двигается подобно маятнику.
|
 Верхние планеты двигаются иначе. Угловое расстояние по эклиптике между Солнцем и планетой может быть от 0° до 180°, все планеты перемещаются между звёздами медленнее, чем Солнце. Когда планета расположена в противоположной Солнцу точке небесной сферы, то такое положение называется ¾ противостояние (оппозиция) планеты (разность эклиптических долгот Солнца и планеты при этом равна 180°), условия для наблюдения планеты в это время наилучшие. Когда долготы солнца и планеты отличаются на 90°, то планета находится в оппозиции. Положения, которые занимают планеты относительно Солнца и Земли называются ¾ конфигурации. Среди различных конфигураций можно выделить несколько особых. На рисунке 4.2 обозначено: 1 - орбита верхней планеты; 2 - орбита Земли (З.); 3 - орбита нижней планеты. Конфигурации нижней планеты: в.с. – верхнее соединение; н.с. - нижнее соединение; В.э. - наибольшая восточная элонгация;
Верхние планеты двигаются иначе. Угловое расстояние по эклиптике между Солнцем и планетой может быть от 0° до 180°, все планеты перемещаются между звёздами медленнее, чем Солнце. Когда планета расположена в противоположной Солнцу точке небесной сферы, то такое положение называется ¾ противостояние (оппозиция) планеты (разность эклиптических долгот Солнца и планеты при этом равна 180°), условия для наблюдения планеты в это время наилучшие. Когда долготы солнца и планеты отличаются на 90°, то планета находится в оппозиции. Положения, которые занимают планеты относительно Солнца и Земли называются ¾ конфигурации. Среди различных конфигураций можно выделить несколько особых. На рисунке 4.2 обозначено: 1 - орбита верхней планеты; 2 - орбита Земли (З.); 3 - орбита нижней планеты. Конфигурации нижней планеты: в.с. – верхнее соединение; н.с. - нижнее соединение; В.э. - наибольшая восточная элонгация;
з.э. - наибольшая западная элонгация.
|
|
4.2 Прохождение внутренних планет по диску Солнца.
Вблизи двух узлов орбиты Меркурий и Венера для наблюдателя с Земли «проходят» по диску Солнца. Для Меркурия в среднем это происходит 14 раз за столетие.. Эти прохождения приходятся на ноябрь и май. За 217 лет происходит 9 майских и 20 ноябрьских прохождений - майские через 13 лет или через 33 года, ноябрьские через 7 или через 13 лет; после каждого майского через 3,5 года происходит ноябрьское прохождение Меркурия по диску Солнца. Последние прохождения: 7 мая 2003 г. и 8 ноября 2008 года, следующие: 9 мая 2016 г. и 11 ноября 2019 года.
Прохождение Венеры происходит не боле двух раз за столетие: через 105,5 лет, затем через 8, через 121,5, через 8 и вновь через 105,5 лет. Последние произошли 8.06.2004 (Рис. 4.3) и 5-6.06.2012 г., следующее произойдёт только в XXII веке.
|

В 1761 году Ломоносов, наблюдая прохождение Венеры, открыл у нее атмосферу. Наблюдая моменты контактов Венеры с краем Солнца из различных пунктов, можно определить параллакс Солнца и расстояние от Солнца до Земли.
4.3 Периоды обращения планет: синодический, звездный (сидеричский)
Синодическим периодом обращения планеты (S) называют промежуток времени между двумя ее последовательностями одноименными конфигурациями.
Звездным (сидерическим) периодом (T) планеты называется промежуток времени, в течении которого планета совершает один оборот вокруг Солнца по своей орбите. Для Земли звездный период называется звездным годом (ТÅ).
Между этими периодами существует математическая связь.
Угловое смещение планеты за сутки равно 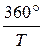 , а у Земли
, а у Земли  , их разность есть видимое смещение планеты за сутки
, их разность есть видимое смещение планеты за сутки 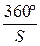 .
.
Отсюда уравнения синодического движения для нижних планет:
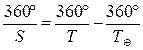 , после сокращения на 360° получим
, после сокращения на 360° получим
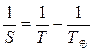 (4.2) ¾ уравнение синодического движения для нижней планеты.
(4.2) ¾ уравнение синодического движения для нижней планеты.
Для верхней планеты запишем:
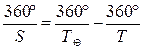 и далее
и далее
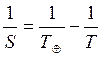 (4.3) ¾ уравнение синодического движения для верхней планеты.
(4.3) ¾ уравнение синодического движения для верхней планеты.
Синодический период можно определить из наблюдений, а звёздный только из вычислений, для земли ТÅ = 365, 26 ср. солн. суток.
Законы Кеплера
Кеплер был сторонником гелиоцентрической системы мира Коперника, и, пытаясь усовершенствовать ее, взялся за обработку многолетних наблюдений планеты Марс, выполненных Тихо Браге и в течение нескольких лет самим И.Кеплером. Первоначально он пытался подобрать круговую орбиту (идеальное движение), но затем путем вычислений вывел, что форма орбиты ¾ эллипс, плоскость которого проходит через Солнце, а само Солнце находится в фокусе эллипса, а движение происходит неравномерно. В начале 1607г. И.Кеплер сформулировал первые два закона:
1. Все планеты движутся по эллипсу вокруг Солнца в одном из фокусов которого (общем для всех планет) находится Солнце (рис.4.4 а)).
|
2. Радиус-вектор планеты за равные промежутки времени описывает равные площади.
Математически этот закон можно записать:
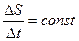 , (4.4)
, (4.4)
где DS ¾ площадь сектора , Dt ¾ промежуток времени (рис. 4.4 б)).
Кроме того Кеплер показал, что плоскости планетных орбит наклонены к эклиптике, причем у каждой планетной орбиты свой наклон.
В 1618г. Кеплер обнародовал свой третий закон планетных движений, выражавший связь между периодом планеты и величиной большой полуоси:
3. Квадраты звездных периодов обращения планет относятся как кубы больших полуосей их эллиптических орбит.
 (4.5)
(4.5)
Свои законы Кеплер вывел эмпирически, т.е. путем подбора не вскрывая причины такого движения.
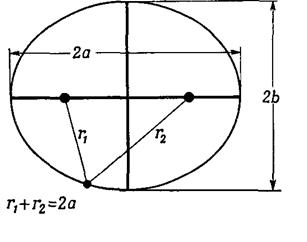
Согласно 1-му закону орбита планет – эллипс, но эллипс есть геометрическое место точек (М), сумма расстояний которых до двух данных точек F1, F2 имеет одно и то же значение 2а, F1М +F2М = 2а где F1, F2 ¾ фокусы эллипса (рис. 4.5). Можно сказать, что сумма r1+r2=const .
|
|
|
|
Движение планеты вокруг Солнца по законам Кеплера ещё называют невозмущенным движением. Путь планеты или другого небесного тела в пространстве называется орбитой. Орбита (орбитальный эллипс) (рис. 4.6) характеризуется определёнными параметрами:
¾ РО=АО - большая полуось а;
¾ в фокусе F1 находится притягивающая масса ¾ Солнце (S);
¾ ближайшая к Солнцу точка орбиты называется перигелий (Р), а наиболее отдаленная – афелий (А);
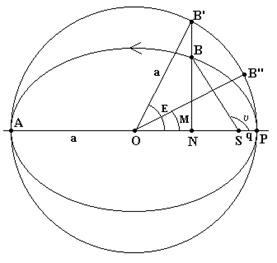
Рис. 4.6 Орбитальный эллипс
¾ 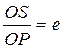 (эксцентриситет), e – характеризует степень сжатия эллипса;
(эксцентриситет), e – характеризует степень сжатия эллипса;
¾ большая ось орбиты АР называется линией (осью) апcид;
¾ отрезок, соединяющий фокус и планету (SB) называется радиус-вектор планеты (r).
Для расстояний от перигелия и афелия до главного фокуса существуют следующие соотношения :
ПS=a(1-e)=q ; (4.6)
AS=a(1+e)=Q ; (4.7)
, где а- большая полуось, равная a=(q+Q)/2 .
Если Vcр средняя орбитальная скорость, то скорость в перигелии Р и афелии А будет равна:

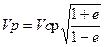 ; (4.8)
; (4.8)
 , (4.9)
, (4.9)
для Земли Vсp =29,78 км/сек., эксцентриситет орбиты Земли 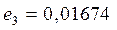 . Если для Земли а=1 и Т=1, то для любой планеты .
. Если для Земли а=1 и Т=1, то для любой планеты .
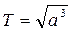 (4.10)
(4.10)
Элементы орбит.
Движение планеты или любого тела, вокруг центрального тела будет определено, если известна плоскость, в которой лежит её орбита, размеры и форма этой орбиты, её ориентировка в плоскости и, наконец, момент времени, в который планета находится в определённой точке орбиты. Величины, определяющие орбиты планеты, называются элементами орбиты.
|
|
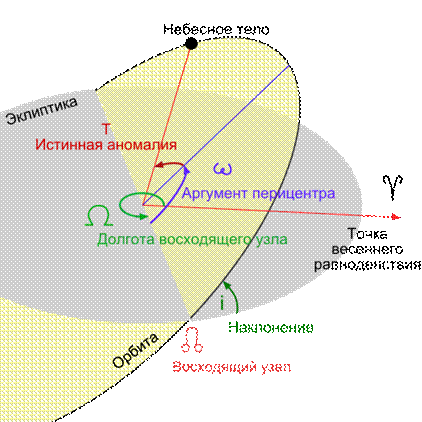
Рис. 4.7 Элементы орбит
Основных элементов 6 (Рис. 4.7):
1) наклон i плоскости орбиты к плоскости эклиптики 0°< i <180°, если 0°< i <180°, то движение прямое; если 90°< i <180° то движение обратное;
2) Долгота восходящего узла Ω; т. угол из центра О между положением на 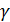 (Т.В.Р) и восходящий узел орбиты Ω; 0°< Ω <360°, элементы i и Ω определяют положение плоскости орбиты в пространстве;
(Т.В.Р) и восходящий узел орбиты Ω; 0°< Ω <360°, элементы i и Ω определяют положение плоскости орбиты в пространстве;
3) ω (аргумент перигея) – угловое расстояние перигелия (аргумент перигелия) от узла до линии апсид (угол из центра Солнца между b и П, он отсчитывается в плоскости орбиты планеты в направлении ее движения, 0°<ω<360°, величина ω определяет положение орбиты в ее плоскости;
4) а– большая полуось эллиптической орбиты, которая определяет звездный период обращения планеты.
5) эксцентриситет орбиты е = 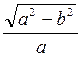 , е – определяет форму эллипса, а и e определяют размеры и форму эллипса;
, е – определяет форму эллипса, а и e определяют размеры и форму эллипса;
6) t0 – момент прохождения через перигелий t0, зная t0 можно определить положение планеты на орбите в любой момент времени.
Положение планеты на орбите определяется двумя величинами: радиус – вектором r и истинной аномалией v, которые вычисляются по формулам, следующим из законов Кеплера,
r = α (1-ecosE); где E – эксцентрическая аномалия, Е=ÐРОВ¢ (рис. 4.5).
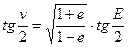 ; (4.11)
; (4.11)
где E – эксцентрическая аномалия, E находят из уравнения Кеплера методом последовательных приближений
M = E – esinE,
где M – средняя аномалии;
M = n(t -t0) = 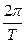 ´(t -t0), (4.12)
´(t -t0), (4.12)
где n – среднее движение планеты, n= 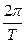 , Т - период обращения.
, Т - период обращения.
Дата добавления: 2021-01-11; просмотров: 1034;











