Определение масс небесных тел

Из механики известно, что для точки, равномерно движущейся по кругу, центростремительное ускорение а_ц = w²R , где w — угловая скорость точки, равная w=2p/Т (Т ¾ период обращения), а R — радиус круга. Принимая орбиту Луны за окружность с приближенным радиусом R = 384000 км, а период обращения Луны вокруг Земли равным примерно 27,3 средних суток (сидерический месяц), получим центростремительное ускорение орбитального движения Луны

.

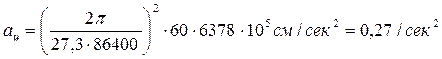Эта значение совпадает с величиной, полученной в разделе (4.6.1) по формулам, вытекающим из закона всемирного тяготения. Для Земли, движущейся вокруг Солнца получим, что её центростремительное ускорение равно а_ц=0,59 см/сек² такое же значение получим из (4.20).

Приравняем центростремительное ускорение какого либо тела к ускорению силы притяжения от другого тела (4.20), движущимся по орбитам вокруг друг друга

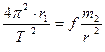. (4.27)

Такое же выражение можно записать и для второго тела

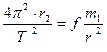. (4.28)

Складывая уравнения (4.27) и (4.28), получим

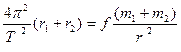, где r₁+r₂=r (4.29)

Преобразуем выражение (4.29)

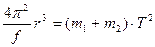. (4.30)

Это выражение справедливо для любых пар тел, например для планеты, обращающейся вокруг Солнца, или для спутника, обращающегося вокруг планеты. Следовательно выражение (4.30) можно записать для систем Солнце ¾ Земля и для Земля ¾ Луна:

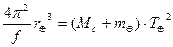, (4.31)

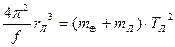, (4.32)

где М_С ¾ масса Солнца, m_Å ¾ масса Земли, m_Å ¾ масса Луны, Т_Å ¾ период обращения Земли вокруг Солнца, Т_Л ¾ период обращения Луны вокруг Земли, r_ž астрономическая единица, а r_Л ¾ расстояние от Земли до Луны. Разделив уравнение (4.31) на уравнение (4.32), получим

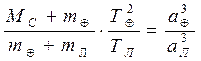. (4.33)

Из (4.33), зная массу Земли можно найти массу Солнца. Из закона всемирного тяготения для Земли

g=ƒ´m_Å/R²; (4.34)

m_Å=g·R²/ƒ (4.35)

По известным g, R и ƒ масса Земли будет

m_Å=5,976×10²⁷г≈6×10²⁷г·, а средняя плотность r≈5,52 г/см³ .

Учитывая, что m_Å многократно меньше М_С (в 333 000 раз), а m_Л меньше m_Å в 81,3 раза , то выражение (4.33) можно переписать как:

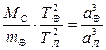, (4.36)

Отсюда М_С можно найти из выражения

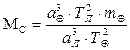. (4.37)

Для любых двух пар притягивающих тел выражение (4.33) можно записать как

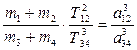. (4.38)

Выражение (4.38) является точной формулой третьего закона Кеплера. Третий уточненный закон Кеплера позволяет определить массу планеты, если у нее есть хотя бы один спутник. В (4.38) массы m_2,4 , как правило, пренебрегаемо малы по сравнению с массами m_1,3, следовательно, зная m₁ или m₃ можно вычислить вторую массу. Однако первоначально необходимо определить m какого либо тела в Солнечной системе, первоначально эта задача была решена для Земли.

Если у какого либо тела спутники отсутствуют, то его масса определяется другими методами, но на основе закона всемирного тяготения. Так массу Луны m_ƒ определили по «лунному неравенству» в долготе Cолнца с месячным периодом. Это следствие того, что центр масс Земля-Луна находится на расстоянии 4650 км от центра Земли в сторону Луны. По приливам определили, что отношение масс Луна-Земля равно

.

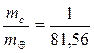По наблюдениям астероидов и затем ИСЗ оно получено как 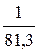. С этим значением M_¤=333000´m_Å , M_¤≈2·10³³г .

Движение ИСЗ

Выведя 4-го октября 1957 года на орбиту вокруг Земли первое, созданное человеком искусственное тело (искусственный спутник Земли ¾ ИСЗ), СССР открыл эру освоения космоса человеком.

Движение ИСЗ происходит по тем же законам, что и естественные тела, но есть и свои особенности, которые следует рассмотреть.

Третья ступень ракеты сообщает ИСЗ определенную скорость V на высоте h. Чтобы спутник вышел на орбиту вокруг Земли эта скорость должна быть больше определенной величины.

Если скорость запуска точно равна круговой скорости на данной высоте h, то тело будет двигаться по круговой орбите. Если эта скорость превышает круговую, то тело будет двигаться по эллипсу, причем перигей этого эллипса окажется в точке выхода на орбиту. Если же сообщенная скорость несколько меньше круговой, а высота h достаточно большая, то тело также будет двигаться по эллиптической орбите, но в этом случае точка выхода на орбиту станет апогеем.

Масса искусственного спутника ничтожно мала в сравнении с массой Земли и ею можно пренебречь; тогда круговая скорость V_C на расстоянии r=R+h от центра Земли согласно (4.26а)) и (4.35) будет

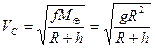. (4.39)

У поверхности Земли при h=0, R=6,37 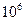м и g=9,81 м/сек² эта скорость, которая называется первая космическая скорость будет равна V_1K=7,91 км/сек. Однако при h=0, существование спутника невозможно и поэтому запуск ИСЗ производится на некоторой высоте h (h > 150 км). Круговая скорость на высоте h меньше первой космической скорости V_1к и определяется из уравнения (4.39).

Для высоты h V_КР=V_1K 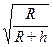, для эллиптической орбиты, учитывая (4.24), получим

,

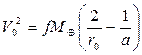Где r₀ ¾ расстояние точки выхода на орбиту от центра Земли, а ¾ большая полуось орбиты.

Эксентриситет орбиты при горизонтальном запуске равен

е=1- ,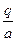

где q ¾ расстояние перигея (ближайшей точки орбиты от центра Земли). Для эллиптической орбиты q=a(1-е)=R+hп, где hп ¾ высота перигея над поверхностью Земли. Расстояние апогея (наиболее удаленной точки орбиты от центра Земли) Q = a (l + e) = R + h_A , где h_A — высота апогея над земной поверхностью. Если запуск произведен в перигее (чего может и не быть), то r₀=q = R + h_П .

На рис. 4.9 приведены несколько типов орбит, в зависимости от начальной

скорости ИСЗ: (I) - V₀=V_круг ; (II) - V₀ <V_круг; (III) - V0 <<V_круг ; (IV) - V₀ >V_круг но V₀ <Vп .

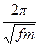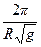T= a= ·a

Для R=6370 км, g=981см/сек² , T_мин=1,659· ·a (a-в км )

Причина изменения орбиты ИСЗ (главная)

1) экваториальное утолщение ;

2) сопротивление атмосферы.

Рис. 4.9 Зависимость формы орбиты от скорости

Для того чтобы КА преодолел притяжение Земли и ушел в космическое пространство, ему необходимо сообщить скорость не менее параболической

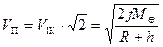, (4.40)

эта вторая космическая скорость, равная

.

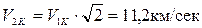Рассчитаем скорость необходимую для выхода за пределы солнечной системы. Круговая скорость Земли V_K =29,8 км/сек, параболическая скорость на расстоянии Земли от Солнца равна:

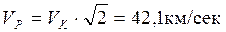, следовательно дополнительная скорость космического аппарата в направлении движения Земли должна быть

V_доп=(42,1-29,8) =12,3 км/сек .

Доказывается, что начальная скорость космического аппарата в этом случае будет

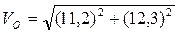, эта скорость называется третья космическая скорость.