Следствия закона всемирного тяготения

Из второго основного закона механики (4.14) и закона всемирного тяготения (4.17) следует:

1. Две материальные частицы, или материальные точки (т.е. материальные тела, размеры которых исчезающе малы по сравнению с расстоянием между ними), притягивают друг друга с одинаковой силой F, но получают при этом разные ускорения, обратно пропорциональные их массам. Действительно, от силы F масса m₁ получает ускорение w₁=f×m₂/r² направленное к m₂ , a масса m₂ — ускорение w₂=f×m2/r² направленное к т₁ . Отсюда

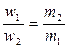. (4.18)

Следовательно, например, ускорение Земли от притяжения ее Луной меньше ускорения Луны от притяжения ее Землей во столько же раз, во сколько раз масса Луны меньше массы Земли.

2. Относительное ускорение двух материальных точек w_от равно разности w₁ - w₂ , и так как w₁ и w₂ направлены в противоположные стороны, то

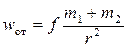, (4.19)

т. е. w_от пропорционально сумме масс частиц. Следовательно, ускорение при относительном движении имеет такую же величину, как и в случае, если бы масса обеих частиц (m₁ + m₂) была сосредоточена в одной из них. Поэтому при решении задачи о движении двух притягивающихся материальных точек можно считать, что сила исходит из неподвижного центра, и исследовать движение только одной точки.

3. Две материальные точки с массами m₁ и т₂ , находящиеся на равных расстояниях от третьей материальной точки с массой т, притягиваются последней с разными силами

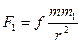и ,

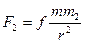но ускорения (по величине) получают одинаковые, равные

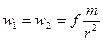. (4.20)

Например, Солнце притягивает Землю с большей силой, чем Луну, но Земля и Луна, когда они находятся на одном и том же расстоянии от Солнца, получают от него одинаковые ускорения.

4. Легко доказать, что сила тяготения и сила тяжести тождественны. Если в (4.20) подставить массу Земли и среднее расстояние от Земли до Луны, то получим ускорение, вызываемое тяготением Земли на Луну

.

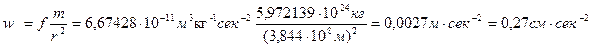Всем телам на поверхности Земли сила тяжести сообщает при их свободном падении ускорение g, равное приблизительно g»981 см/сек2., если сила тяжести изменяется обратно пропорционально квадрату расстояния тела от центра Земли, то Луна, находящаяся от центра Земли на расстоянии в 60 земных радиусов (приблизительно), должна испытывать ускорение g' в 60² раз меньшее, чем ускорение на поверхности Земли, т.е.

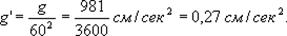
5. Сила тяжести на поверхности Земли есть равнодействующая двух сил: силы притяжения, направленной к центру массы Земли, и центробежной силы, направленной перпендикулярно к оси вращения Земли. Так как Земля сплюснута вдоль оси вращения, то сила притяжения у полюсов больше, чем в других местах, и уменьшается к экватору. Кроме того, центробежная сила действует против силы притяжения. Поэтому сила тяжести на поверхности Земли уменьшается при переходе от полюсов к экватору.

Разница в ускорении силы тяжести между полюсами и экватором составляет g_90° -g_0° = 983,2 — 978,0 = 5,2 см/сек². Около 2/3 этой разности возникает за счет центробежного ускорения на земном экваторе и около 1/3 — за счет сплюснутости Земли. Среднее значение ускорения силы земной тяжести принимается равным g = 981 см/сек².

Результаты измерений ускорения силы тяжести в различных точках земной поверхности показали отклонения (возмущения) силы тяжести по сравнению с ее нормальным значением, соответствующим эллипсоиду, а также уклонением вектора силы тяжести (отвесной линии) от нормали к эллипсоиду. Эти отклонения называются аномалиями силы тяжести и уклонениями отвеса и объясняются тем, что строение земной коры неоднородно как в отношении видимых наружных масс (горных массивов и т.п.), так и в отношении плотностей горных пород, составляющих земную кору. Ряд мелких неоднородностей в строении верхних слоев земной коры вызывают местные аномалии силы тяжести, охватывающие небольшие районы. Местные аномалии свидетельствуют о наличии залежей ископаемых, обладающих либо очень большой плотностью (например, руды металлов) либо очень маленькой плотностью (например, залежи нефти, каменной соли). Такие аномалии и уклонения помогают в поиске полезных ископаемых.

Сила тяжести измеряется также под поверхностью Земли (шахты, скважины) и под водой. Таким образом изучается гравитационное поле Земли, этим занимается наука гравиметрия.