Лекция 12. Развитие небесной механики.

Задача двух тел.

Цель:рассмотрение задачи движения в центрально симметричном поле и законов Кеплера как ее следствие.

Ключевые слова: гео - и гелиоцентрическая системы мира, закон Всемирного тяготения, задача двух тел.

Структура:

1. Составляющие небесной механики.

2. Общая и ограниченная задача двух тел.

3. Обобщенные законы Кеплера.

Физические основы:

1. Динамика. Масса и сила как основные понятия динамики.

2. Законы И. Ньютона.

3. Закон Всемирного тяготения.

4. Движение в поле центральной силы.

5. Форма траекторий в поле центральной силы.

6. Интегралы движения и законы сохранения.

7. Космические скорости.

Начало возникновения и развития небесной механики можно отнести к периоду системы мира Птолемея (геоцентрической системы). Принятие гелиоцентрической системы мира сопровождалось исследованием доказательств годичного движения Земли вокруг Солнца, что привело к представлению о возможности не только круговых, но и эллиптических орбит, формулировке эмпирических законов движения планет. Теория тяготения И. Ньютона, его закон всемирного тяготения дали возможность исследования широкого круга наблюдаемых естественных явлений (возмущенное движение, приливы и отливы и другие), определения массы некоторых небесных тел. Закон всемирного тяготения и разработанная на его основ теория движения тел в поле центральной силы применимы не только к движению небесных тел но и к движению созданных человеком космических аппаратов (схема 7).

Схема 7. Развитие небесной механики

Основные закономерности в поступательном движении естественных и искусственных небесных тел можно установить из исследования движения двух тел под действием силы взаимного тяготения.

Если массы двух тел сопоставимы, то такая задача называется общей задачей двух тел; если массой одного из тел можно пренебречь, то задача называется ограниченной задачей двух тел.

Решение задачи двух тел в приложении к телам Солнечной системы, а также к двойным звездам на достаточно больших промежутках времени дает удовлетворительное согласие теории с наблюдениями. Это обстоятельство объясняется особенностями динамического строения Солнечной системы, а именно:

1. Достаточная взаимная удаленность тел Солнечной системы, обеспечивающая возможность замены реальных тел материальными точками.

2. Малость масс всех тел планетарной системы по сравнению с массой Солнца, что позволяет на первом этапе изучения движения планет учитывать только Солнечное притяжение и пренебрегать притяжением других больших планет.

3. Близость фигур Солнца и больших планет к сферам, допускающая независимое рассмотрение поступательного и вращательного движения тел планетной системы.

На практике достаточно изучить лишь движение одной точки относительно системы координат с началом в другой точке. Поэтому возьмем систему координат 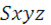с неизменными направлениями осей и с началом в притягивающей точке S массой М. В соответствии с законами классической механики уравнение Ньютона для второй из точек Р массой m запишется в форме:

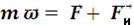, (1)

где 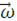- относительное ускорение точки Р, 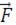- сила ньютоновского тяготения, а 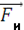- сила инерции, вызванная поступательным движением системы координат 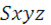ускоренно всесте со своим началом относительно какой-либо инерциальной системы отсчета.

В согласии с законом тяготения Ньютона модуль силы 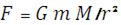, где 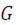– постоянная тяготения, а 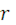- расстояние точки Рот начала координат. Направление этой силы задается единичным вектором - . Поэтому 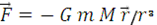. На точку 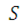действует противоположно направленная сила - 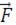. Тогда ускорение поступательного движения системы координат равно 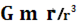. Умножая это ускорение на массу точки Р и изменяя знак произведения, получим, что

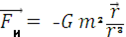
Теперь, подставив найденные значения сил 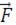и 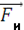в соотношение (1), после упрощений приходим к уравнению относительного движения:

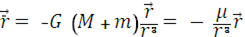. (2)

В ограниченной задаче двух тел при m « M μ = GM.