Часть 2. Возмущение эллиптических орбит.

В астрономии, как и в физике легко решается задача двух взаимодействующих сил. Она сводится к задаче движения в центрально – симметричном поле. Если бы тела Солнечной системы притягивались только Солнцем, то их движение вокруг Солнца точно определялось бы законами Кеплера. Такое движение называется невозмущенным. В действительности все тела взаимодействуют между собой. Каждое тело находится в поле тяготения всех других тел, поэтому на каждое тело действует несколько сил, и все они являются переменными вследствие относительного движения тел. Эти взаимодействия создают отклонения от строгих орбит определяемых центрально – симметричной силой: круговых, эллиптических, параболических, гиперболических. Отклонения движения тел от идеальных орбит называют возмущенным, а реальное движение называется возмущенным движением. Возмущение тел Солнечной системы имеют сложный характер. Их учет очень труден, не смотря на то, что сами возмущения не велики вследствие малой массы тел по сравнению с массой Солнца. Общая масса тел Солнечной системы составляет 1/700 массы Солнца. Возмущение рассматривается как различие между положением тела при возмущенном и не возмущенном движениях, а возмущенное движение – движение по законом Кеплера с переменными элементами орбиты. Изменения элементов орбиты тела, вследствие притяжения его другими (кроме центрального) телами называются возмущениями или неравенствами элементов. Эти вопросы решаются в соответствующей задаче, называемой задачей многих тел (трех и более тел).Вопросы, связанные с возмущением в движении тел Солнечной системы можно представить в виде схемы (схема 10).

Схема 10. Возмущенное движение.

Задача многих тел. Возмущенное движение планет

В природе невозможно указать пару гравитирующих тел, движение которых совершенно строго описывалось бы решением задачи двух тел. При точном анализе движения приходится учитывать возмущения от других притягивающих тел.

На каждое тело Солнечной системы действует большое количество других тел (в частности планет или их спутников). Однако, действующие силы существенно различны по величине. Их можно упорядочить так, что каждая последующая хотя бы на порядок меньше предыдущей. В этом случае применим метод возмущений, который состоит в следующем. Вначале решается задача двух тел (нулевое приближение), учитывается действие на исследуемое тело только основной силы (например Солнце). В полученное решение вносится поправка на действие следующей по порядку величины силы. Получают решение в первом приближении. В это решение вносится поправка на действие следующей силы и так далее. В астрономии разработаны математические методы внесения поправок методом последовательных приближений до необходимой точности. Поэтому наряду с задачей двух тел в астрономии рассматривается задача трех тел, а часто и задача n (многих) тел. В них речь идет об анализе движения надлежащего числа взаимно тяготеющих точечных масс. Количество тел, составляющих рассматриваемую систему, определяется физическими соображениями. Необходимо, чтобы систему nтел с большой степенью точности можно было бы считать замкнутой и изолированной.

В задаче nтел необходимо найти 3nкоординат в виде явных функций времени. Так как каждая из координат определяется дифференциальным уравнением второго порядка, то общий порядок системы уравнений движения составляет 6n.

Задача допускает 10 классических интегралов уравнений движения. Их существование вытекает из общих теорем динамики системы.

Так как в системе тяготеющих тел все силы внутренние, то центр масс системы движется прямолинейно и равномерно (в инерциальной системе координат). Если через 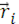обозначить радиус – вектор массы 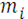, то длярадиус – вектора 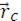и скорости 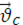- центра масс системы тел – справедливы соотношения:

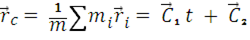и = ,

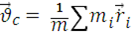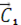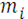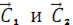в которых m = Σ , а - произвольные векторные постоянные. Проектируя эти векторные интегралы на оси координат, получим шесть скалярных интегралов движения центра масс.

Поскольку главный момент действующих сил равен нулю, то момент количества движения систем постоянен:

.

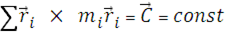Последнее векторное уравнение в проекциях на оси координат дает три интеграла площадей.

Наконец, в согласии с законом сохранения полной механической энергии запишем интеграл энергии

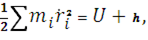
где 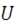- потенциал сил взаимного тяготения, а 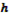- произвольная постоянная.