Часть 1. Характеристики эллиптических орбит.

Законы И. Кеплера, согласно которым планеты двигаются по эллиптическим орбитам, в фокусе которых находится Солнце, соответствует гелиоцентрической системе мира и закону Всемирного тяготения. Движение планеты определено, если известны плоскость в которой лежит ее орбита, размеры и форма этой орбиты, ее ориентация в плоскости и момент времени в который планета находится в определенной точке орбиты. Величины, определяющие орбиту планеты, называются элементами ее орбиты. Положение плоскости орбиты определяется относительно плоскости эклиптики, то есть относительно плоскости орбиты Земли. Две точки, в которых орбита планеты пересекается с плоскостью эклиптики, называются узлами: восходящие и нисходящие. Эллиптическая орбита планеты определяется шестью элементами (рис. 36).

Обозначения:

а, в – большая и малая полуоси эллипса

r – радиус – вектор

Р = а (1- 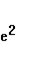) )– фокальный параметр

Θ- истинная аномалия

е = – эксцентриситет

0 ≤ е ≤1

1) 0 ≤ е <1, (h<0) - эллипс (е=0 окружность)

2) е=0, (h=0) - парабола

3) е>1, (h>0) - гипербола.

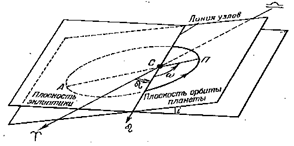
Рис 36. Элементы эллиптических орбит

Элементы орбиты –величины, определяющие орбиту планеты.

Основная плоскость,относительно которой определяется положение орбиты – плоскость эклиптики.

Узлы –(восходящие и нисходящие) – две точки, в которых орбита планеты пересекается с плоскостью эклиптики.

Восходящий узел –тот, в котором планета пересекает эклиптику, удаляясь от южного пояса.

Элементы орбиты:(их 6)

1) Наклонение іорбиты к плоскости эклиптики

0 ≤ i< 90 -прямое восхождение

90 <i< 180 -обратное движение.

2) Долгота (гелиоцентрическая) Ω

3) Угловое расстояние ωперигелия от узла.

4) а– большая полуось эллиптической орбиты, однозначно определяет сидерический период обращения.

5) е– эксцентриситет орбиты е =

6) t₀ –момент прохождения через перигелий (или долгота в эпоху t)

Можно выделить основные задачи теоретической астрономии относящихся к движению планет (схема 9).

Схема 9. Задачи теоретической астрономии.

Таким образом, решение физической задачи движения в центрально – симметричном поле существенно продвинуло развитие астрономии. Можно отметить, что эта задача сыграла также важную роль в решении проблемы атома в модели Резерфорда.