Экспериментальное определение закона распределения
В таблицах представлены измеренные значения размеров партии заготовок. Сгруппируем результаты измерений в интервалы с величиной, равной 0,02 мм, и занесём их в таблицу 3.3.
Таблица 3.3
Действительные размеры наружных поверхностей вращения для выборки из партии заготовок
| № пп | Действитель-ный размер, мм | № пп | Действитель- ный размер, мм | № пп | Действитель-ный размер, мм | № пп | Действитель-ный размер, мм | № пп | Действитель- ный размер, мм |
| 14,98 14,96 14,97 14,99 14,96 14,95 15,01 14,96 14,96 14,98 | 14,93 14,95 14,97 14,98 14,96 14,96 14,92 14,97 14,95 14,95 | 14,96 14,98 14,93 14,96 14,97 15,00 14,96 14,97 14,95 14,94 | 14,95 14,96 14,91 14,93 14,96 14,96 14,94 14,95 14,97 14,97 | 14,96 14,89 14,95 14,96 14,98 14,99 14,96 14,95 15,00 14,94 |
Таблица 3.4
Результаты промежуточных расчетов для интервалов размеров
| Интервал размеров, мм | Середина интервала
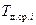 , мм , мм
| Частота
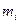
| Произведение
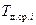 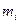 , мм , мм
| Разность
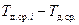 , мм , мм
| Произведение
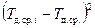 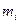
| |
| нижняя граница | верхняя граница | |||||
| 14,89 14,91 14,93 14,95 14,97 14,99 15,01 | 14,91 14,93 14,95 14,97 14,99 15,01 15,03 | 14,90 14,92 14,94 14,96 14,98 15,00 15,02 | 14,90 29,84 89,64 359,04 179,76 60,00 15,02 | – 0,06 – 0,04 – 0,02 0,00 0,02 0,04 0,06 | 0,0036 0,0032 0,0024 0,0000 0,0048 0,0064 0,0036 |
По приведённым выше формулам рассчитаем:
а) статистическое среднеарифметическое значение размеров заготовок
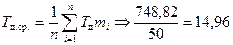 ;
;
б) оценку статистического среднеквадратического отклонения определяется на основании данных размеров партии заготовок
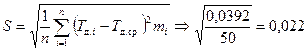 ;
;
в) теоретическое среднее квадратичное отклонение
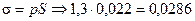 .
.
г) теоретическое поле рассеяния размеров
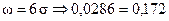 мм;
мм;
д) теоретические значения максимального и минимального размеров
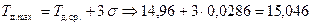 .
.
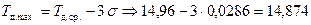 .
.
Построить эмпирическую кривую и теоретическую кривую распределения.
Теоретическая кривая распределения имеет максимум, равный
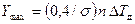 .
.
на расстоянии 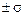 от вершины кривая имеет две точки перегиба, ординаты которых
от вершины кривая имеет две точки перегиба, ординаты которых
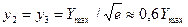 .
.
При практических расчётах обычно принимается, что на расстоянии 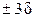 от положения вершины ветви кривой нормального распределения пересекаются с осью абсцисс
от положения вершины ветви кривой нормального распределения пересекаются с осью абсцисс 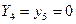 .
.
Подставив конкретные значения рассматриваемого примера, получим:
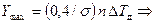
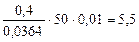 ;
;
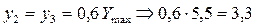 .
.
Полученные значения ординат откладываем на графике и соединяем плавной кривой 3.
Установить возможность отбора без брака.
Сопоставляя 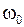 и
и 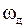 , констатируем
, констатируем 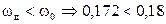 . Это значит, что, во-первых, выбор ТСО анализа осуществлен правильно. Во-вторых, ТСО действительно способна обеспечить получение размера поверхности с заданными точностными требованиями. При этом действительный запас точности
. Это значит, что, во-первых, выбор ТСО анализа осуществлен правильно. Во-вторых, ТСО действительно способна обеспечить получение размера поверхности с заданными точностными требованиями. При этом действительный запас точности
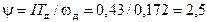 .
.
Проверяя условие 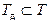 и
и 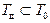 , получаем (14,874; 15,046) и (14,57; 15,0), то есть имеет место выход действительных размеров за максимально допустимый размер.
, получаем (14,874; 15,046) и (14,57; 15,0), то есть имеет место выход действительных размеров за максимально допустимый размер.
Определим вероятность получения брака. Площадь, ограниченная кривой нормального распределения и осью абсцисс, равна единице и представляет 100% заготовок партии. Площадь заштрихованных участков характеризует собой количество (в долях единицы или в %) заготовок, выходящих по своим размерам за пределы поля допуска. Практически для определения количества годных заготовок необходимо найти площадь, ограниченную кривой и осью абсцисс на длине, равной допуску
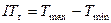 .
.
Это можно сделать, используя значения функции Лапласа 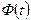 , которые приведены в [1] приложении в зависимости от величины нормированного параметра t. Для определения исправимого и неисправимого брака величина определяется выражениями
, которые приведены в [1] приложении в зависимости от величины нормированного параметра t. Для определения исправимого и неисправимого брака величина определяется выражениями
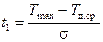 ;
; 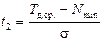 .
.
Тогда вероятностный процент брака определяется по формуле
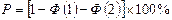 ,
,
в том числе исправимого брака
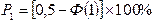 ,
,
неисправимого брака
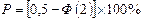 .
.
Для рассматриваемого примера найдем значения
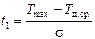
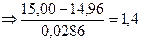 ;
;
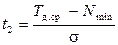
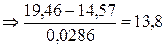 .
.
Тогда 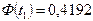 ;
; 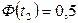 . Вероятностный процент брака составит:
. Вероятностный процент брака составит:
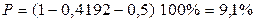 ;
;
исправимого
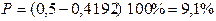 ;
;
неисправимого
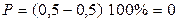 .
.
Вопросы для самопроверки
1. Дайте определение множества.
2. Как задать множество?
3. Что такое пустое множество?
4. Как обозначить объединение множеств?
5. Как записывается условие несовместимости событий?
6. Как записывается полная группа событий
7. Назовите виды статистических распределений.
8. Назовите основные числовые характеристики статистической выборки.
9. Назовите числовые характеристики выборочного распределения.
10. Что такое полигон распределения?
11. Что такое гистограмма распределения?
12. Что такое генеральная совокупность?
13. Что такое математическое ожидание?
Дата добавления: 2021-01-11; просмотров: 522;











