Статистическая оценка законов распределения случайных величин
Эмпирические ряды распределения, получаемые при обработке первичных статистических данных, оформляются в таблицах или изображаются графически посредством геометрических образов – точек, линий и фигур в различных сочетаниях. Построение эмпирических графиков и диаграмм позволяет установить на первом этапе исследования к какому типу теоретических распределений ближе всего полученное эмпирическое распределение, что облегчает выбор конкретных технических приемов обработки исходных данных.
Для применения графического метода анализа распределений необходимо знать, как строить графики распределения, какие существуют типы распределений и какими свойствами обладают теоретические распределения.
Покажем, каким образом производится обработка статистического материала для нахождения законов распределения случайной величины. Для этого будем рассматривать некоторую случайную величину X. При функционировании экономической системы или ее элемента в течение некоторого времени t случайная величина X может принять п определенных значений. Совокупность этих случайных значений случайной величины в математической статистике называется статистической выборкой объема п. Если расположить отдельные значения случайной величины X в возрастающем или убывающем порядке и указать относительно каждого значения, как часто оно встречалось в данной совокупности, то получится эмпирическое распределение случайной величины, или вариационный ряд, на основании которого определяются аналитическая форма неизвестной плотности вероятности f (x), функция распределения F (x)и оцениваются входящие в нее параметры.
Рассмотрим подробнее процедуру построения вариационного ряда.
Весь диапазон значений непрерывной случайной величины X разбивается на интервалы. Далее подсчитывается количество значений mi случайной величины Х, приходящейся на каждый интервал, и определяется частота ее попадания в данный интервал по формуле
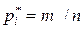 .
.
Если случайная величина X принимает значение, попадающее на границу i-го и (i+1)-го интервалов, то это значение учитывается в числе попаданий в (i+1)-й интервал.
Определив таким образом частоты попадания случайной величины X в каждый интервал, получим вариационный (статистический) ряд, который представлен в табл. 3.
Вариационный ряд
Оптимальная длина интервала определяется по формуле
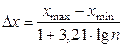
где хmax – хmin – размах вариации случайной величины X.
Число интервалов будет равно:
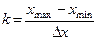
Если k не целое число, то в качестве числа интервалов надо взять ближайшее к k целое число, не меньшее k.
Вариационные ряды могут быть изображены графически в виде полигона распределения и гистограммы.
Полигон распределения представляет собой многоугольник, который строится на прямоугольной координатной сетке следующим образом. В выбранных масштабах на оси абсцисс наносится шкала для фактических значений случайной величины X,на оси ординат – для частот 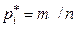 (рис. 1). Пользуясь этими шкалами, наносят точки Mi с координатами xi и mi /n.
(рис. 1). Пользуясь этими шкалами, наносят точки Mi с координатами xi и mi /n.
Точки 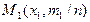 ,
, 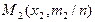 , … ,
, … , 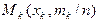 соединяют ломаной линией M1 M2 M3… Mi … Mk .Крайние точки M1 и Mk , если они не лежат на оси 0х, соединяют со смежными точками соответственно
соединяют ломаной линией M1 M2 M3… Mi … Mk .Крайние точки M1 и Mk , если они не лежат на оси 0х, соединяют со смежными точками соответственно 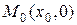 и
и 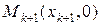 на оси абсцисс.
на оси абсцисс.
Таким образом, полученный многоугольник M0 M1 M2 M3… Mi … Mk, Mk+1является полигоном распределения.
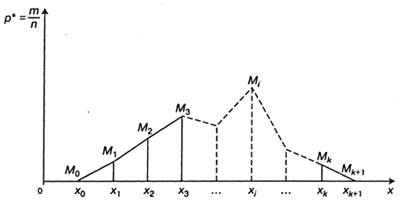
Рис. 3.2. Полигон распределения реализаций случайной величины X
Полигоны распределения чаще всего применяются для изображения дискретных вариационных рядов.
Гистограмма распределения реализаций случайной величины применяется для графического изображения интервальных рядов распределения. Она представляет собой многоугольник, построенный с помощью смежных прямоугольников. В случае непрерывных равных интервалов с шириной интервала ∆х гистограмма строится следующим образом (рис. 3.3).
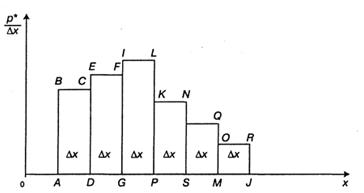
Рис. 3.3. Гистограмма распределения
В выбранных масштабах на оси абсцисс наносится шкала для реализаций случайной величины X, на оси ординат – величины p*/∆х. Пользуясь этими шкалами, строят прямоугольники ABCD, DEFG,..., основания которых соответствуют ширине интервала ∆х, а высоты равны отношениям p1*/∆х, p2*/∆х, … , pk*/∆х.
Многоугольник ABCEF... QORJA и является гистограммой распределения.
Гистограммы чаще всего применяются для изображения вариационных рядов с непрерывными значениями случайной величины X. При уменьшении величины каждого интервала гистограмма будет приближаться к некоторой плавной кривой, соответствующей графику функции плотности распределения случайной величины X. Следовательно, в результате построения гистограммы можно получить представление о дифференциальном законе распределения случайной величины X.
Эмпирическая (статистическая) функция распределения строится следующим образом. Над каждым отрезком оси абсцисс (∆х), изображающим расстояние между концами интервалов, проводится отрезок горизонтальной прямой на уровне ординаты, равной величине накопленной частоты; концы горизонтальных отрезков соединяются вертикальными линиями.
Статистическая функция распределения F*(X)представляет собой частоту событий Х < х в данной выборке:
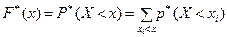 ,
,
где х – текущая величина, 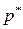 – частота, или статистическая вероятность, события.
– частота, или статистическая вероятность, события.
Неравенство xi < х под знаком суммы указывает, что суммирование распространяется на все те значения xi, которые меньше х. Значения F*(xj)при данном значении xj определяется по формуле
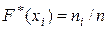
где ni – число опытов, при которых X < xi.
При неограниченном увеличении числа опытов (наблюдений) п согласно теореме Я.Бернулли при любом xi частота события р*(Х < xi) приближается (сходится по вероятности) к вероятности этого события. Следовательно, если X – непрерывная величина, то при увеличении п график функции F*(х) приближается к плавной кривой F(x) – интегральной функции распределения величины X. Таким образом, графическое изображение рядов распределения
дает возможность наглядно представить эмпирическое распределение реализаций случайной величины и выразить закономерность ее распределения путем построения статистической интегральной функции распределения.
Пример.Построить гистограмму и статистическую функцию распределения часовой выработки подвижного состава автопредприятия.
Значения часовой выработки получены в ходе наблюдения за работой автомобилей-самосвалов КамАЗ-5511 в течение календарного года. Объем выборки составил n = 100 наблюдений. Размах вариации равен:
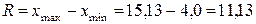 .
.
Величина интервала вариационного ряда определена по формуле
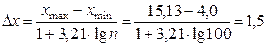 .
.
Число интервалов интервала вариационного ряда равно:
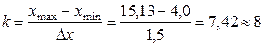 .
.
Вариационный ряд часовой выработки автомобиля представлен в табл. 3.1
| Интервал ∆хim | 4 – 5,5 | 5,5 – 7,0 | 7,0 – 8,5 | 8,5 - 10 | 10 - 11,5 | 11,5 – 13,0 | 13,0 – 14,5 | 14,5 - 16 |
| Частота Pi* | 0,07 | 0,14 | 0,17 | 0,17 | 0,15 | 0,14 | 0,17 | 0,05 |
Решение
Для построения гистограммы определим ее ординаты из выражения
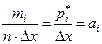 .
.
Отсюда находим
1) 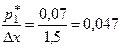 ; 2)
; 2) 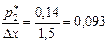 ; 3)
; 3) 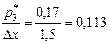 ;
;
4) 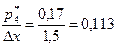 ; 5)
; 5) 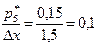 ; 6)
; 6) 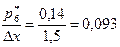 ;
;
7) 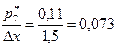 ; 8)
; 8) 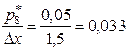 .
.
Основываясь на данных табл. 3.1 и проведенных расчетах, построим гистограмму (рис. 3.4).
Следует отметить, что при неограниченном увеличении объема выборки п кривая гистофаммы частот совпадает с графиком плотности вероятностей.
Построим статистическую функцию распределения часовой выработки автомобиля:
1) при х ≤ 4 F*(x1)= 0;
2) при 4 < х ≤ 5,5 F*(x2)= 0,07;
3) при 5,5 < х ≤ 7 F*(x3)= 0,21;
4) при 7 < х ≤ 8,5 F*(x4)= 0,38;
5) при 8,5 < х ≤ 10 F*(x5)= 0,55;
6) при 10 < х ≤ 11,5 F*(x6)= 0,70;
7) при 11,5 < х ≤ 13 F*(x7)= 0,84;
8) при 13 < х ≤ 14,5 F*(x8)= 0,95;
9) при 14,5 < х ≤ 16,0 F*(x9)= 1,0.
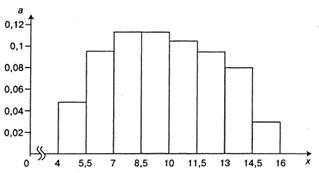
Рис. 3.4 Гистограмма часовой выработки автомобиля
График статистической функции распределения представлен на рис. 3.5.
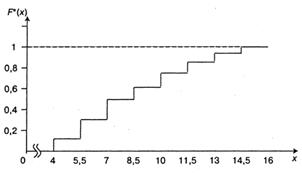
Рис. 3.5 Статистическая функция распределения часовой выработки автомобиля
Статистическая функция распределения случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны эмпирическим вероятностям этих значений.
Сумма всех скачков функции F*(x)равна единице. По мере увеличения объема выборки и уменьшения интервалов ∆х число скачков становится больше, а сами скачки – меньше; ступенчатая кривая становится более плавной; случайная величина постепенно приближается к непрерывной величине, а ее статистическая функция распределения – к непрерывной функции – интегральной функции распределения F(x).
Дата добавления: 2021-01-11; просмотров: 588;











