Числовые характеристики случайных величин

При решении многих практических задач часто достаточно указать отдельные числовые характеристики, определяющие особенности того или иного распределения случайной величины. Это, прежде всего, среднее значение, которое принадлежит к характеристикам положения случайной величины, т. е. представляет такую величину, относительно которой каким-то образом группируются, рассеиваются всевозможные значения случайной величины.

Математическое ожидание является теоретической характеристикой случайной величины.

Эмпирическая средняя случайной величины по мере увеличения испытаний (наблюдений) приобретает тенденцию стабилизироваться относительно постоянной величины - математического

ожидания. Для непрерывной случайной величины X математическое ожидание определяется интегралом:

.

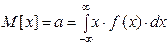Кроме математического ожидания на практике иногда применяются и другие характеристики положения, в частности медиана и мода случайной величины.

Медианой Me случайной величины называется такая величина, относительно которой равновероятно получение большего или меньшего значения случайной величины:

.

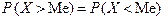Медиану применяют в качестве характеристики ряда распределения в тех случаях, когда имеются очень большие колебания случайной величины. В этом случае на эмпирическую среднюю М*[Х] будут оказывать сильное влияние крайние значения случайной величины, а медиана менее чувствительна к крайним значениям случайной величины. На медиану влияет не столько колебание в значениях случайной величины X, сколько колебания в частоте появления того или иного значения случайной величины.

Модой Мо дискретной случайной величины называется ее значение, обладающее наибольшей вероятностью. Для непрерывной случайной величины мода есть такое значение, которое отвечает

максимальной плотности распределения.

В общем случае математическое ожидание, медиана и мода не совпадают. В частном случае при симметричном распределении все три характеристики положения случайной величины совпадают.

Для оценки степени разброса, рассеивания значений случайной величины относительно среднего вычисляют следующие характеристики:

• дисперсию;

• среднее квадратическое отклонение;

• коэффициент вариации.

Дисперсией называется математическое ожидание квадрата отклонений случайной величины от своего математического ожидания:

.

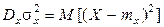Чем больше дисперсия, тем в среднем больше отклонение значений случайной величины относительно математического ожидания, т. е. будет больше рассеивание случайной величины.

Дисперсия дискретной случайной величины вычисляется по формуле

.

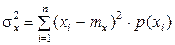Дисперсия непрерывной случайной величины равна:

.

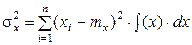Наряду с дисперсией случайной величины, в качестве характеристики рассеивания случайной величины используется среднее квадратическое отклонение, которое равно положительному значению корня квадратного из дисперсии.

Среднее квадратическое отклонение имеет одинаковую размерность со случайной величиной, в этом состоит ее преимущество относительно дисперсии.

Эмпирические значения характеристик рассеивания вычисляют по формулам:

дисперсия

.

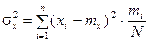среднее квадратическое отклонение

.

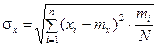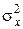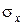Величины и показывают абсолютное отклонение от среднего значения случайной величины, что недостаточно характеризует уровень ее рассеивания. Относительной характеристикой рассеивания является коэффициент вариации, вычисляемый как отношение среднего квадратического отклонения и эмпирической средней

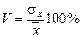или .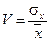

Коэффициент вариации может использоваться для сравнения меры рассеивания случайных величин, имеющих различную размерность.