Методика статистических исследований для оценки точности обработки деталей

Закон распределения хорошо иллюстрируется кривой рассеяния размеров, которая строится следующим образом. Измеренные значения размеров партии заготовок разбиваются на ряд интервалов. Ширина интервала выбирается в зависимости от точности размеров детали таким образом, чтобы число интервалов было не меньше шести (при числе измеряемых заготовок в партии не менее 50 шт.). Для каждого интервала подсчитывается частность повторения размеров 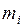, то есть отношение количества заготовок, действительные размеры которых попали в данный интервал, к общему числу заготовок.

По оси абсцисс откладываются интервалы размеров, и на каждом из интервалов, как на их основании, строится прямоугольник. Высота прямоугольника определяется делением частности на ширину интервала ( 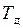). Полученная ступенчатая линия называется гистограммой распределения. При последовательном соединении между собой точек, соответствующих середине каждого интервала, образуется ломаная линия, которая называется эмпирической кривой распределения, или полигоном. По полученным статистическим данным определяют следующие характеристики:

1. Среднее арифметическое действительных размеров заготовок:

.

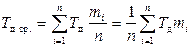2. Оценка среднего квадратичного отклонения размеров, определяемая на основании данных размеров партии заготовок:

.

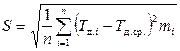В большинстве случаев при механической обработке заготовок с точностью 8...10-го квалитетов и грубее при обеспечении её методом групповой (настройка на партию) настройки кривая рассеяния размеров получает очертание, удовлетворяющее закону нормального распределения (закону Гаусса).