Методы и модели корреляционно-регрессионного анализа
Большинство явлений и процессов находятся в постоянной взаимной объективной взаимосвязи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ.
Различают два вида зависимостей между явлениями и процессами:
• функциональную;
• стохастическую (вероятностную, статистическую).
В случае функциональной зависимости имеется однозначное отображение множества А на множество В. Множество А называют областью определения функции, а множество В – множеством значений функции.
Функциональная зависимость встречается редко. В большинстве случаев функция (Y)или аргумент (Х) – случайные величины. X и Y подвержены действию различных случайных факторов, среди которых могут быть факторы, общие для двух случайных величин.
Если на случайную величину Х действуют факторы Z1, Z2, ..., V1, V2, а на Y - Z0, Z2, V1, V3 ..., то наличие двух общих факторов Z2и V1 позволит говорить о вероятностной или статистической зависимости между Х и Y.
Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.
В частном случае статистическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание другой. В этом случае говорят о корреляции или корреляционной зависимости.
Статистическая зависимость проявляется только в массовом процессе, при большом числе единиц совокупности.
При стохастической закономерности для заданных значений зависимой переменной можно указать ряд значений объясняющей переменной, случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обусловливается тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов.
Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью. Односторонняя вероятностная зависимость между случайными величинами есть регрессия. Она устанавливает соответствие между этими величинами.
Односторонняя стохастическая зависимость выражается с помощью функции, которая называется регрессией.
Виды регрессий
1.Регрессия относительно числа переменных:
• простая регрессия – регрессия между двумя переменными;
• множественная регрессия – регрессия между зависимой переменной у и несколькими объясняющими переменными х1, х2, …, xm.
Множественная линейная регрессия имеет следующий вид:
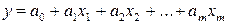 ,
,
где у – функция регрессии; х1, х2, …, xm – независимые переменные; a1, a2, …, am – коэффициенты регрессии; a0– свободный член уравнения; m – число факторов, включаемых в модель.
2. Регрессия относительно формы зависимости:
• линейная регрессия, выражаемая линейной функцией;
• нелинейная регрессия, выражаемая нелинейной функцией.
Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова. Если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляция.
Понятия «корреляция» и «регрессия» тесно связаны между собой.
Корреляционный и регрессионный анализ имеют свои задачи.
Задачи корреляционного анализа
1.Измерение степени связности (тесноты, силы) двух и более явлений. Здесь речь идет в основном о подтверждении уже известных связей.
2. Отбор факторов, оказывающих наиболее существенное влияние на результативный признак на основе измерения тесноты связи между явлениями.
3. Обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждений об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных рассуждений, раскрывающих механизм связей.
Задачи регрессионного анализа
1.Установление формы зависимости (линейная или нелинейная; положительная или отрицательная и т. д.).
2. Определение функции регрессии и установление влияния факторов на зависимую переменную. Важно не только определить форму регрессии, указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов, если бы прочие не изменялись и если бы были исключены случайные элементы. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.
3. Оценка неизвестных значений зависимой переменной, т. е. решение задач экстраполяции и интерполяции. В ходе экстраполяции распространяются тенденции, установленные в прошлом, на будущий период. Экстраполяция широко используется в прогнозировании. В ходе интерполяции определяют недостающие значения, соответствующие моментам времени между известными моментами, т. е. определяют значения зависимой переменной внутри интервала заданных значений факторов.
Этапы построения многофакторной корреляционно-регрессионной модели
Разработка модели и исследование процессов должны выполняться по следующим этапам:
1) априорное исследование экономической проблемы;
2) формирование перечня факторов и их логический анализ;
3) сбор исходных данных и их первичная обработка;
4) спецификация функции регрессии;
5) оценка функции регрессии;
6) отбор главных факторов;
7) проверка адекватности модели;
8) интерпретация;
9) прогнозирование неизвестных значений зависимой переменной.
Планирование эксперимента
В настоящее время благодаря развитию математической теории экспериментов появилась возможность применения математических методов не только при обработке результатов наблюдений, но и при планировании экспериментального исследования. Планирование эксперимента – это постановка опытов по некоторой заранее составленной схеме, обладающей какими-то оптимальными свойствами. Разработка таких схем представляет собой сложную математическую задачу.
В отличие от наиболее распространенного однофакторного метода исследований, когда изучается действие каждого фактора в отдельности, применение метода планирования эксперимента позволяет при исследовании сложных процессов выполнять эксперименты так, чтобы варьировать все факторы сразу. Это способствует повышению эффективности эксперимента, выражающейся в том, что интересующие экспериментатора параметры определяются со значительно меньшей ошибкой, чем при традиционных методах исследования. При этом с повышением числа факторов повышается точность эксперимента.
При планировании эксперимента должны быть определены: необходимое число опытов, последовательность проведения эксперимента, математическая модель для описания эксперимента.
При составлении плана проведения экспериментального исследования для каждой независимой переменной выбирается определенное число уровней варьирования. Поэтому необходимое число опытов определяется числом возможных комбинаций уровней варьирования независимых переменных, а также количеством повторных опытов.
Для планируемого эксперимента важную роль играет последовательность выполнения опытов. В целях усреднения эффектов от неконтролируемых переменных, сопутствующих любому экспериментальному исследованию (например, от изменения напряжения в сети, неоднородности обрабатываемого материала и материала режущего инструмента и т.д.) отдельные опыты следует проводить в случайной последовательности, которая может быть определена, например, с помощью таблиц случайных чисел, лотереи, путем бросания игральной кости или других способов.
Сложнее решается вопрос выбора математической модели, описывающей эксперимент. В наиболее общем случае исследуемый процесс можно изобразить в виде некоторого «черного ящика».

Рис. 2. Представление процесса в виде «черного ящика»,
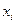 – входной параметр процесса (фактор),
– входной параметр процесса (фактор), 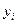 – выходной параметр процесса (выход, целевая функция).
– выходной параметр процесса (выход, целевая функция).
Необходимо выбрать модель процесса. Это уравнение, связывающее выход с факторами
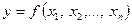 . (2.1)
. (2.1)
Функцию (2.1) называют функцией отклика.
Выбор связан с утверждением о возможности представления любой аналитической функции в виде полинома. Например, для двух факторов можно выбрать полином первой степени
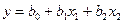 , (2.2)
, (2.2)
второй степени
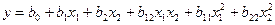 , и т.д. (2.3)
, и т.д. (2.3)
где 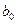 ,
, 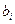 ,
, 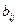 – коэффициенты полинома.
– коэффициенты полинома.
Полиномы (2.2), (2.3) называют уравнениями регрессии. Коэффициенты полинома определяются экспериментом. Важный вопрос: какой выбрать полином на первом шаге? Если мы хотим получить интерполяционную модель, с помощью которой можно предсказать результат во всех точках выбранной области параметров. Целесообразно начинать с линейной модели. Если она окажется неадекватной, то следует увеличить степень полинома. Особенность решаемой задачи в том, что выражение (2.3) после его логарифмирования позволяет выбрать линейную модель полинома.
Рассмотрим применение метода планирования эксперимента для исследования зависимости силы резания 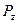 от режимов резания (
от режимов резания ( 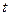 ,
, 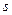 ,
, 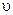 ). Особенность решения такой задачи в том, что многочисленные исследования показали возможность аппроксимации этой зависимости в виде степенной функции, которая при многофакторном эксперименте имеет вид
). Особенность решения такой задачи в том, что многочисленные исследования показали возможность аппроксимации этой зависимости в виде степенной функции, которая при многофакторном эксперименте имеет вид
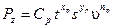 , (2.4)
, (2.4)
где 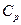 ,
, 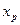 ,
, 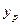 ,
, 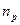 – коэффициенты, подлежащие экспериментальному определению.
– коэффициенты, подлежащие экспериментальному определению.
После логарифмирования выражения (2.4) получим линейную модель исследуемого процесса
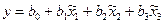 , (2.5)
, (2.5)
где 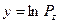 ;
; 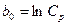 ;
; 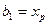 ;
; 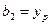 ;
; 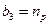 ;
; 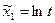 ;
; 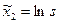 ;
; 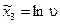 .
.
Теперь только останется разумно построить эксперимент, чтобы определить коэффициенты уравнения (2.3).
Теперь только остается разумно построить эксперимент, чтобы определить коэффициенты уравнения (2.5). Далее для достижения поставленной цели будем действовать по следующему плану.
1. Выбор интервалов варьирования факторов.
2. Составление плана эксперимента и его проведения.
3. Вычисление коэффициентов уравнения регрессии и получение зависимости для определения силы резания.
1. Общие требования к факторам: управляемость и однозначность. Требования к совокупности факторов: совместимость и отсутствие линейной зависимости. Эти требования для выбранных факторов удовлетворяются.
Теперь рассмотрим дальнейшие шаги, которые надо выполнить в общем случае.
Поскольку выбранная модель линейна, то для каждого фактора необходимо выбрать два уровня, на которых он будет варьироваться. Один из этих уровней называют верхним, другой – нижним. Между этими двумя уровнями находится так называемый основной уровень. Введем еще одно понятие: интервал варьирования. Это некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычисление – нижний уровни. Интервал варьирования не может быть меньше той ошибки, с которой фиксируется уровень фактора. С другой стороны он не должен выходить за область определения фактора. Иногда выбор интервалов варьирования связан с интуитивными решениями, основанными на опыте экспериментатора. Так или иначе, выбор интервалов варьирования скажется на адекватности выбранной модели процесса.
В данной работе интервалы варьирования определяются сравнительно узким диапазоном измерения факторов. Для упрощения записи плана эксперимента и обработки его результатов факторы кодируются. При этом верхнему уровню соответствует код « 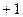 », а нижнему – «
», а нижнему – « 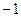 », а основному «
», а основному « 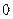 ». Этого можно добиться с помощью преобразования
». Этого можно добиться с помощью преобразования
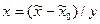 , (2.6)
, (2.6)
где 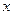 – кодированное значение фактора;
– кодированное значение фактора; 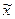 – натуральное значение фактора;
– натуральное значение фактора; 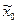 – натуральное значение основного (нулевого) уровня;
– натуральное значение основного (нулевого) уровня; 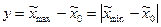 – натуральное значение интервала варьирования;
– натуральное значение интервала варьирования; 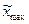 ,
, 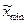 – соответственно натуральные значения верхнего и нижнего уровней.
– соответственно натуральные значения верхнего и нижнего уровней.
2. План эксперимента строится на варьировании каждого фактора на двух уровнях. Все возможные комбинации уровней (число опытов N) определяются зависимостью N = 2 k, где 2 – это число уровней; 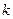 – число факторов. В нашем случае N = 23 = 8. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Каждый столбец в этой матрице называется вектор столбцом, а каждая строка вектор-столбцом. Геометрической интерпретацией эксперимента 23 является куб. Этот куб задает область эксперимента, а центр куба определяет основной (нулевой) уровень. После некоторых рассуждений матрица планирования претерпит некоторые изменения. Они связаны с процедурой расчета коэффициентов уравнения регрессии.
– число факторов. В нашем случае N = 23 = 8. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Каждый столбец в этой матрице называется вектор столбцом, а каждая строка вектор-столбцом. Геометрической интерпретацией эксперимента 23 является куб. Этот куб задает область эксперимента, а центр куба определяет основной (нулевой) уровень. После некоторых рассуждений матрица планирования претерпит некоторые изменения. Они связаны с процедурой расчета коэффициентов уравнения регрессии.
3. При расчете коэффициентов 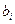 следует обратить внимание на следующее. Эксперимент, содержащий конечное число опытов, дает только выборочные оценки коэффициентов. Их точность нуждается в статистической проверке. Поэтому формула, приведенная ниже, дает оценки коэффициентов уравнения регрессии
следует обратить внимание на следующее. Эксперимент, содержащий конечное число опытов, дает только выборочные оценки коэффициентов. Их точность нуждается в статистической проверке. Поэтому формула, приведенная ниже, дает оценки коэффициентов уравнения регрессии
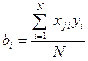 , (2.7)
, (2.7)
где 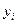 – значение выхода в «
– значение выхода в « 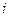 » опыте;
» опыте; 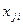 – значение «
– значение « 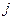 » фактора в «
» фактора в « 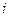 » опыте.
» опыте.
С помощью этой формулы определим для примера коэффициент 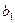 . То есть для подсчета оценки коэффициента
. То есть для подсчета оценки коэффициента 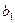 использовался вектор-столбец
использовался вектор-столбец 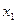 . Для вычисления
. Для вычисления 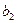 ,
, 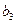 потребуются вектор-столбцы
потребуются вектор-столбцы 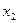 ,
, 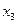 . Как найти
. Как найти 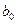 ? Для ответа на этот вопрос рассуждения таковы. Если уравнение (2.3) справедливо, то есть адекватно описывает процесс, то оно верно и для средних значений факторов. Но средние значения кодированных факторов равны нулю. Поэтому
? Для ответа на этот вопрос рассуждения таковы. Если уравнение (2.3) справедливо, то есть адекватно описывает процесс, то оно верно и для средних значений факторов. Но средние значения кодированных факторов равны нулю. Поэтому 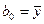 , то есть
, то есть 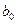 равен среднему значению выхода процесса. Для удобства определения коэффициента
равен среднему значению выхода процесса. Для удобства определения коэффициента 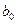 в уравнении (2.3)
в уравнении (2.3) 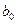 умножим на коэффициент
умножим на коэффициент 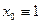 , а в матрицу планирования введем дополнительно вектор-столбец
, а в матрицу планирования введем дополнительно вектор-столбец 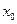 . При этом добавим два эксперимента в центре плана. В итоге получим
. При этом добавим два эксперимента в центре плана. В итоге получим
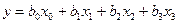 . (2.8)
. (2.8)
Рассмотрим пример.Пусть элемент режима резания меняются в пределах: 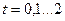 мм;
мм; 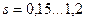 мм/об;
мм/об; 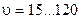 м/мин. В соответствии с уравнением (8) и выражением (9) определим кодовые значения факторов.
м/мин. В соответствии с уравнением (8) и выражением (9) определим кодовые значения факторов.
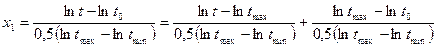 .
.
Вследствие симметричности плана эксперимента второе слагаемое в правой части равно 1. Поэтому окончательно получим
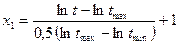 . (2.9)
. (2.9)
Аналогичным образом получим
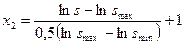 . (2.10)
. (2.10)
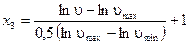 . (2.11)
. (2.11)
Для принятых диапазонов изменения выражения (13) - (15) примут вид
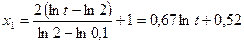 ;
;
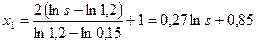 ;
;
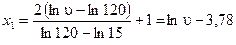 .
.
Матрица планирования вместе с матрицей исходных данных и результатами экспериментов приведены в табл. 2.
По выражению (2.10) определяем коэффициенты уравнения регрессии
Вопросы для самопроверки
1. Какие различают два вида зависимостей между явлениями и процессами
2. Определите понятие планирование эксперимента.
3. Какую модель использует метод наименьших квадратов и как она связана с его названием? Каков алгоритм метода?
4. Что изучает дисциплина математическая статистика?
5. Перечислите простейшие характеристики распределения случайной величины.
6. Поясните понятия корреляция и регрессия.
7. Что означает термин «черный ящик»?
8. Что называют «функция отклика»?
9. Что должно быть определено при планировании эксперимента?
10. Что называется полным факторным экспериментом?
11. Что является геометрической интерпретацией полного факторного эксперимента?
12. Чему равно число комбинаций факторов в трехфакторном эксперименте
13. Напишите уравнение регрессии для двухфакторного эксперимента.
14. Что такое интервал варьирования?
15. Что такое нормированные факторы?
16. Назовите требования к факторам и требования к совокупности факторов.
Дата добавления: 2021-01-11; просмотров: 514;











