Проектирование нечетких контроллеров

Проектирование нечетких регуляторов требует принятия решений о выборе значительно большего числа субъектов проектирования, чем проектирование традиционных («четких») регуляторов. Эти решения касаются, например, выбора базовых правил, механизма (алгоритма) инференции, способа дефаззификации, предварительной и конечной обработки данных. Данный раздел определяет (устанавливает) и описывает методику проектирования нечеткого контроллера, включенного в одноконтурную систему управления. Раздел содержит также технологию проектирования, которая использует ПИД-регулятор как отправную точку.

Основные понятия

В то время как относительно просто осуществить проектирование четкого ПИД-регулятора, использование нечетких правил поднимает целый ряд проблем, и хотя многие литературные источники (написанные в основном на английском языке) разъясняют сущность нечеткого управления, уделим внимание глобальным принципам, которыми надо руководствоваться при выборе параметров простых нечетких регуляторов. Так как конечным результатом практической деятельности по проектированию системы является задача цифровой реализации алгоритма нечеткого управления, т.е. создание управляющего контроллера, в дальнейшем будем называть нечеткие регуляторы нечеткими контроллерами. Описываемый в этом разделе подход базируется на трехступенчатой процедуре проектирования, рассматриваемой применительно к ПИД-управлению. Вот эти три шага (ступени).

1. Спроектировать четкий ПИД-регулятор.

2. Заменить ПИД-регулятор эквивалентным линейным нечетким контроллером.

3. Преобразовать последний контроллер в нелинейный нечеткий контроллер.

Мы познакомим вас с различными компонентами нечеткого контроллера и связанными с ними задачами проектирования. В следующих трех параграфах опишем три простых способа реализации (построения) нечетких контроллеров, а именно: контроллер, построенный с использованием таблиц преобразования; контроллер, использующий преобразование вход-выход, и контроллер типа Такаги-Сугено. Краткое заключение обобщает основные процедуры и проблемы проектирования простых нечетких контроллеров в виде списка проблем. Этот список может служить как справочный для проектировщика системы управления.

Нечеткие системы широко используются для широкого круга применений в технике, науки, бизнесе, медицине, психологии и других областях. Например, в технике, некоторые многообещающие области применения включают в себя:

· Летательные аппараты/космические аппараты: Управление полетом, управление двигателями, авиационные электронные системы, обнаружение отказов и неисправностей.

· Автоматизация дорожного движения: Автоматическое управление направлением движения, торможением и дросселированием клапанов транспортных средств.

· Автономные транспортные средства: Навигация наземных и подводных транспортных средств.

· Управление промышленными процессами: Планирование и управление производственными процессами (управление печью для отжига цемента, метро и т.д.).

· Производство промышленных товаров: Стиральные машины, видеокамеры, плиты для быстрого приготовления риса.

· Электроэнергетика: Управление двигателями, распределение мощности/энергии и оценка нагрузки.

· Робототехника: Регулирование положения, разработка траекторий движения.

Нечеткое управление базируется на нечеткой логике. Так же как нечеткая логика может быть описана как «вычисления, осуществляемые скорее с помощью слов, чем чисел (цифр)», нечеткое управление можно трактовать «как управление, осуществляемое скорее с помощью высказываний, чем уравнений». Нечеткое управление может включать в себя эмпирические правила и что особенно полезно правила, опирающиеся на опыт операторов объектов управления (управляемых процессов).

Рассмотрим, например, типичный нечеткий контроллер с набором правил.

1. Если ошибка Отр и скорость изменения ошибки Отр,

То управляющее воздействие (выход нечеткого контроллера) ОтрБ. (2.1)

2. Если ошибка Отр и скорость изменения ошибки Нуль,

То управляющее воздействие ОтрС.

Набор правил называется базовыми правилами или нечеткой базой знаний. Эти правила представлены в знакомой вам форме Если-То. Общепринято называть часть правил, стоящую за словом Если, предпосылкой (условием), а часть правил, расположенную за словом То, – заключением (следствием) (однако более часто эта пара называется антецедент-консеквент или предпосылка-заключение). Значение входа «Отр» есть лингвистический терм, сокращение слова Отрицательная, значение выхода «ОтрБ» означает Отрицательно Большой, а значение выхода «ОтрС» означает Отрицательно Средний. Компьютер в состоянии использовать (выполнять) правила и вычислять управляющее воздействие в соответствии с измеренными с помощью датчиков физическими (количественными) значениями ошибки и скорости изменения ошибки.

Мы ставим своей целью показать и разъяснить будущему инженеру различные процедуры проектирования.

В базовых правилах для нечеткого контроллера стратегия (закон) управления представлена на более или менее естественном языке. Причем каждое из правил, входящих в набор правил, не связано с другими правилами, как бы изолировано от них. Напротив, система уравнений, описывающих обычный (четкий) контроллер, включает в себя связанные между собой уравнения. Базовые правила просты для понимания и просты для применения конечными пользователями, даже неспециалистами в области управления. Эквивалентный контроллер может быть реализован с помощью обычной технологии – по сути дела, контроллер, основанный на базовых правилах, может быть эмулирован на язык программирования, скажем, на C – это как раз удобно, чтобы обособить закон управления в базовых правилах для оператора системы управления.

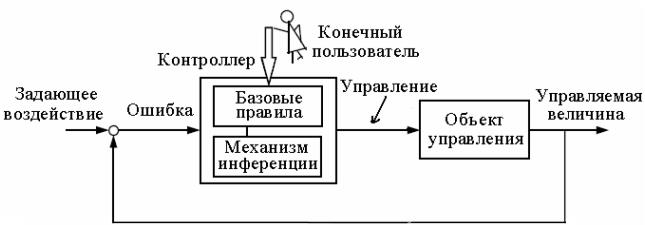
Рис. 2.1

Нечеткие контроллеры используются в различных вариантах функциональных схем систем управления. Самым распространенным вариантом является управление по ошибке или прямое управление с обратной связью, когда нечеткий контроллер располагается в прямой цепи системы с единичной обратной связью (рис. 2.1). Выход объекта управления (управляемая величина) сравнивается с задающим воздействием (желаемым значением управляемой величины) и если имеет место ошибка управления (отклонение), то контроллер вырабатывает управляющее воздействие в соответствии с законом (стратегией) управления. На рис. 2.1 линии со стрелками могут означать двойные линии со стрелками, содержащие зараз несколько сигналов для управления многомерным объектом. Назначение других элементов, представленных на этом рисунке, поясним несколько позже. Сейчас же заметим, что контроллер на схеме является нечетким контроллером, и он заменяет обычный (четкий) контроллер, другими словами, последовательное корректирующее устройство, скажем, ПИД-регулятор.

Продемонстрируем работу нечеткого ПИ-регулятора на примере управления уровнем жидкости в баке (симулятор, вызываемый с помощью файла flc.exp. в папке Мои документы/УМК/ flc.exp). Управляемая величина y(t); возмущающие воздействия: приток Q_i (t) и отток Q_o (t); управление U(t); входом нечеткого контроллера являются ошибка E(t) и ее производная dE(t)/dt, обозначаемая в симуляторе как dE(t); выходом контроллера производная управления dU (t)/dt, обозначаемая как dU(t). Всего используется 49 правил и 7 термов для каждой входной и выходной переменной. Можно осуществлять масштабирование входов и выхода за счет изменения универсумов.

При управлении по возмущающему воздействию (рис. 2.2) происходит компенсация измеряемого возмущающего воздействия. Такой закон требует знания достаточно точной модели объекта управления, однако если получение подобной математической модели сопряжено с большими трудностями или с большими экономическими издержками, то можно попытаться использовать нечеткую модель объекта управления. На рис. 2.2 показаны четкий контроллер (регулятор) и нечеткий регулятор, ради простоты опущен объект управления и обратная связь. Управляющее устройство, представленное на этом рисунке и компенсирующее влияние возмущающего воздействия, можно рассматривать

Рис. 2.2

как параллельное соединение линейного и нелинейного контроллеров (регуляторов). В качестве линейного контроллера К может фигурировать ПИД-регулятор, а в качестве нелинейного Н – нечеткий контроллер.

Нечеткие правила могут быть использованы также для подстройки (коррекции) параметров управляющего устройства (контроллера) в адаптивных параметрических системах управления (рис. 2.3).

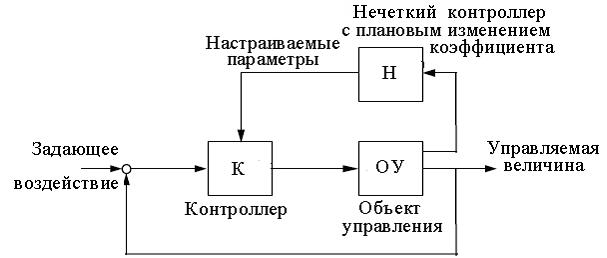
Рис. 2.3

Если меняется рабочая точка нелинейного объекта управления (величина задающего воздействия в промышленных системах управления), то в принципе можно изменять параметры контроллера применительно к каждому новому значению рабочей точки. Как пример, ниже приведена таблица настройки параметров ПИД-регулятора в зависимости от трех значений управляемой величины, в данном случае уровня жидкости в баке (ОУ)

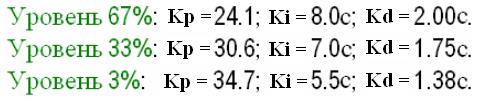
Этот закон управления получил название плановое (табличное) изменение коэффициента (gain scheduling) [10], т.к. первоначально данный закон применялся для изменения коэффициента усиления контроллера в соответствии с заранее рассчитанными и внесенными в таблицу его (коэффициента усиления) значениями.

Контроллер с плановым изменением коэффициента содержит линейный контроллер K, параметры которого изменяются как функция координат рабочей точки. Разумеется, эта функция предварительно определена и запрограммирована, для чего требуется всестороннее знание свойств объекта управления. Тем не менее, описанный подход во многих случаях является эффективным способом уменьшения влияния на управляемую величину нелинейностей и вариации параметров ОУ. Измерения выхода, полученные с помощью датчика, используются как плановые переменные, управляющие изменением параметров контроллера, часто за счет применения табличной формы, которая представляет значения параметров как функции координат рабочей точки (см. выше).

Лекция 8

Продвинутые методы нечеткого управления промышленными объектами. Рассмотрим в общих чертах несколько многообещающих методов управления, основанных на нечетких технологиях, которые, как ожидается, позволят решить многие проблемы, возникающие при управлении объектами в современном промышленном производстве.

1. Нечеткое инверсное управление. Самый простой метод спроектировать нечеткий контроллер, используя принцип разомкнутого управления (без обратной связи), в котором нечеткий контроллер является инверсией объекта управления (обратным объектом управления) (см. рисунок ниже). В случае нелинейной модели объекта в результате получаем нелинейный нечеткий контроллер и, следовательно, в идеале приходим к абсолютно инвариантной системе.

Пусть ОУ описывается нелинейным уравнением

y[i+1]=f(x[i],u[i]),

где

x[i]=(y[i-1],…,y[i-n+1], u[i],…,u[i-m+1])^’.

Выбирая контроллер

u[i]=f ^-1(x[i],v[i+1]),

получаем

y[i+1]=v[i+1].

Однако мы должны иметь в виду, что объект может обладать большим временем чистого запаздывания и это обстоятельство следует учитывать, и что для получения инверсной модели надо очень хорошо знать другие динамические и статические свойства объекта. Кроме того, надо понимать, что окончательная модель объекта никогда не будет точной копией реального объекта, и всегда имеют место воздействующие на объект возмущения, которые не были приняты в расчет при моделировании.

Если нелинейная нечеткая модель найдена для частично неопределенного и весьма сложного по своим свойствам объекта, мы сталкиваемся с трудной проблемой получения инверсной модели. Кроме того, мы должны иметь в виду, что алгоритм для вычисления инверсной модели должен быть весьма быстрым, чтобы можно ее было использовать в реальном времени.

Часто в качестве модели ОУ используют синглтонную нечеткую модель (см. далее). Этот тип модели принадлежит к общему классу аппроксиматоров функций. Другим типом модели, которая может быть точно инвертирована, является модель типа Такаги-Сугено.

Мы должны помнить, что метод, основанный на инверсии, можно только применять к устойчивым ОУ с минимально-фазовыми свойствами.

Мы обычно подразумеваем частичную, а не глобальную инверсию.

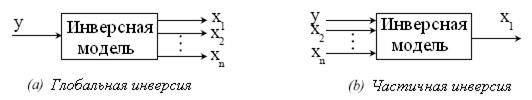
Это означает, что в случае использования нечеткой модели для объекта с одним входом и одним выходом, для которой (нечеткой модели) дополнительными входами являются переменные состояния x₁,x₂,…,x_n, только одна из переменных состояния x₁ становится выходом инверсной модели, и выход модели y становится входом инверсной модели (см. рисунок выше).