Типы материалов и виды расчетов, используемых в универсальных пакетах

Рассмотрим подробнее типы материалов, которые используются при конечно-элементных расчетах. Предварительно напомним некоторые определения из теории упругости. Материал называется изотропным (isotropic), если его свойс­тва одинаковы во всех направлениях. Если свойства материала зави­сят от выбранного направления – то это анизотропный (anisotropic) материал. Анизотропный материал называется ортотроп­ным (orthotropic), если имеются 3 взаимно ортогональных плоскости симметрии, относительно которых его характеристики постоянны, но не равны между собой. Ярким примером ортотроп­ного материала могут служить дерево или композиты.

Строго говоря, большинство материалов, используемых в машиностроении, являются анизотропными. Например, механические свойства прокатанного листа зависят от его ориентации при прокатке (вдоль листа – поперек листа). При обычных расчетах проще считать тот же стальной лист изотропным, но для ответственных деталей, выполняемых с минимальными запасами по прочности, необходимо учитывать анизотропию материала, обусловленную технологической наследственностью.

С механической точки зрения материалы, используемые при МКЭ-расчетах, можно классифицировать также по виду зависимости между напряжением s и деформацией D при приложении нагрузки и, что важно, при ее снятии. Различают упругие и пластические материалы.

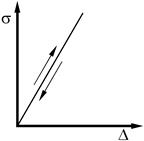
Упругий материал после снятия нагрузки возвращается в исходное состо­яние по той же самой траектории, как и при нагружении (рисунок 35.1, а, б). Остаточная деформация для него равна нулю.

Если между напряжением и деформацией для материала существует линейная зависимость (выполняется закон Гука), то такой материал называют линейно-упругим (рисунок 35.1, а). При этом деформация линейно зависит от напряжения как при приложении, так и при снятии нагрузки. Примером такого материала может служить сталь, когда напряжения в материале не превышают предела пропорциональности.

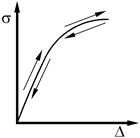
Нелинейно-упругий (non-linear elastic) материал имеет не­линейные, но однозначные зависимости между напряжением и деформацией, одинаковые при нагрузке и разгрузке (рисунок 35.1, б). После разгрузки тело восстанавливает свою форму и размеры без остаточных (пластических) деформаций. Примером такого материала может служить чугун. Разновидностью нелинейно-упругого материала является высокоэластичный (hyperelastic) материал. Он способен упруго выдерживать большие деформации, при которых относительная деформация достигает 500%. Примером такого материала может служить резина, нейлон.

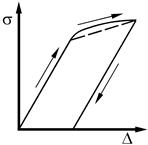
Зависимость деформации от напряжений для упруго-пластичного (elasto-plastic, bi-linear) материала имеет начальный упругий участок, за которым следует зона упрочнения (рисунок 35.1, в). Считается, что разгрузка происхо­дит по прямой, параллельной упругому участку. В результате после снятия нагрузки в теле остаются пластические деформации. Диаграмму деформирования обычно аппроксимируют двумя линейными зависимостями с разными модулями упругости на упругом участке и в зоне упрочнения (штриховая линия на рисунке 35.1, в, которая аппроксимирует нелинейную зависимость в зоне упрочнения).

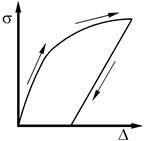
Разновидностью упруго-пластичного материала является пластичный (plastic) материал, диаграмма напряжений которого в общем случае не имеет упругого участка (рисунок 35.1, г). При задании упругих свойств таких материалов их диаграмма напряжений стандартно аппроксимируется не двумя, а несколькими линейными участками.

а)	б)	в)	г)

Рисунок 35.1 – Зависимости между напряжением s и деформацией D для различных материалов

При необходимости можно задать свойства материала по произ­вольной аналитической зависимости напряжение–деформация, или, например, теплопроводность–температура (только как функцию од­ного параметра). При желании можно создать новый материал со своими уникальными механическими и/или тепловыми свойствами. При использовании универсального конечно-элементного пакета в одной модели можно использовать практически любое количество различных материалов.

Виды конечно-элементных расчетов. Статические расчеты. Расчеты, в том числе и конечно-элементные, можно разделить на статические и динамические. В свою очередь, оба эти вида расчетов могут быть линейные и нелинейные.

При статических расчетах предполагается, что внешняя нагрузка и параметры материала не зависят от времени. При динамических расчетах либо нагрузка, либо свойства материала меняются во времени.

В случае линейной модели исследуемой системы результат решения прямо пропорционален величине внешнего воздействия. Например, прогиб балки линейно зависит от величины приложенной силы. В инженерной практике наиболее часто используется статический линейный расчет. Но для наиболее точного отражения поведения реального объекта необходимо использовать нелинейные и, желательно, динамические расчеты.

Для механических систем выделяют три основных вида нелинейности:

1) геометрическая нелинейность, вызванная тем, что перемещения элементов механической системы под нагрузкой становятся сравнимы с размерами самой системы;

2) физическая нелинейность, вызванная зависимостью свойств материала от истории нагружения;