Моделювання СМ в ортогональній системі координат

Істотного спрощення математичної моделі можна досягти відповідним перетворенням змінних і застосуванням систем відносних одиниць. Основний вид перетворення вживаний в СМ є представлення систем диференціальних рівнянь в прямокутній, жорстко пов'язаній з ротором, координатній системі осей dq. Перетворенням піддаються струми, напруги і потокосцепленія статора, наприклад для фазних струмів:

;

;

.

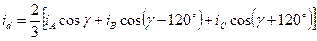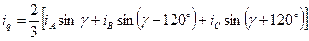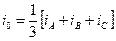Змінні роторних обмоток зазвичай залишаються тим самим і не перетворяться, оскільки вони вже зорієнтовані по осях dq.

Якщо замінити по формулах перетворення струми, потокосцепленія і напруга статора в рівняннях СМ, то після щодо складних перетворень отримаємо нову систему рівнянь у фізичних величинах.

;

;

;

;

;

;

;

;

;

;

;

;

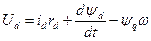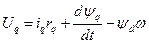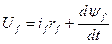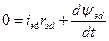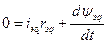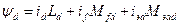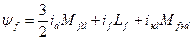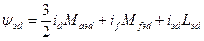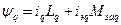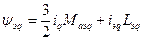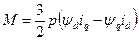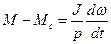Тут позначено:

;

.

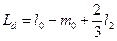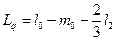Величини напруги 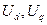можуть бути визначені за допомогою формул перетворення по відомих залежностях реальних фазової напруги. Так якщо останні виражаються гармонійними функціями

;

;

.

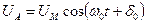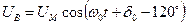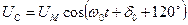де 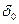початкова фаза включення мережевої напруги, то в перетвореному вигляді

;

.

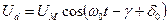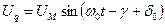На практиці зазвичай використовуються рівняння синхронної машини, записані у відносних одиницях. В даний час базові величини обмоток статорів загальноприйняті, а роторних обмоток у різних авторів різні. При приведенні до відносних одиниць роторних величин найбільш поширеної є, так звана, "система одиниць 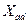" або системою рівний взаїмоїндуктівностей.

Система рівнянь СМ у відносних одиницях матиме вигляд:

;

;

;

;

;

;

;

;

;

;

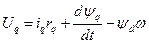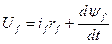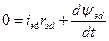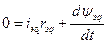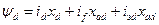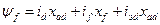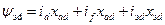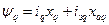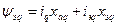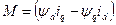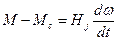
Тут ;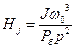

Ці рівняння можуть бути покладені в основу математичної моделі, проте реалізувати їх у такому вигляді скрутно, оскільки ускладнюється визначення струмів в контурах. Для їх визначення необхідно заздалегідь вирішувати систему рівнянь потокосцепленій щодо струмів в контурах.

Зв'язок між струмами і потокосцепленіямі виражається наступною системою рівнянь:

;

;

;

;

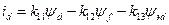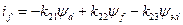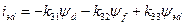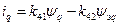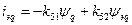
Коефіцієнти 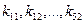є функціями параметрів СМ

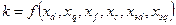
де 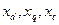- індуктивні опори по подовжній і поперечній осі, опір розсіяння; 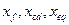- індуктивні опори обмотки збудження і демпферної обмотки по подовжній осі.

Знаходження значень цих опорів менш трудомістко, чим власних і взаємних індуктівностей. Опори зв'язані між собою і з різними постійними часу, які приводяться в каталожних даних.

; ; ;

; ; ;

; ; ;

; ; ; ;

;

.

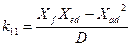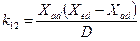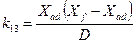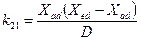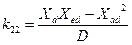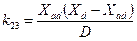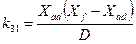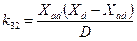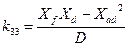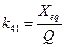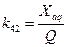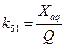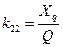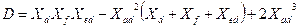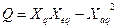Ці рівняння разом з диференціальними рівняннями контурів статора і рівняння динаміки є математичною моделлю СМ.

Основний недолік системи - неможливість моделювання СМ з преобразовательными агрегатами. Це можливо тільки у фазних координатах.

Переваги - спрощення рівнянь і зменшення їх кількості.

Зв'язати струми і напругу в двох координатних системах можна наступними виразами:

- модуль вектора напруги, що зображає

;

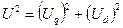- модуль вектора струму, що зображає

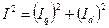
- активна потужність

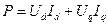
- реактивна потужність

;

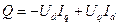ДЛЯ прикладу, побудуємо процеси асинхронного пуску синхронного двигуна СДЕ-15-34-6У2, з наступними паспортними даними::

Параметр	значення	Параметр	значення	Параметр	значення
			0,0874		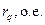0,005
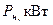
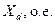
			0,847		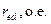0,051
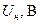
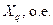
			0,463		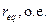0,021
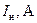
	71,5		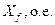0,889		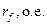0,002
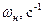
	104,7		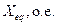0,436
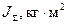
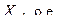
			0,828

У асинхронному режимі 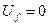, а обмотка збудження замикається на п'ятикратний розрядний опір .

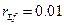На малюнках представлені результати моделювання

Отримані перехідні процеси а) - кутовій швидкості w(t); б) - електромагнітного моменту M(t); в)і г) - модуля вектора струмів статора, що зображає 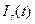; і ротора .

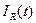Розділ 8.