Моделювання СМ у фазній системі координат
СМ є найскладнішою електричною машиною в плані моделювання, із-за наявності на роторі однофазної обмотки збудження, і, в окремих випадках, пускової (демпферною) обмотки.
Існують різні моделі і схеми заміщення, проте при дослідженнях відволікаються від другорядних явищ і приймають ряд допущень:
1. магнітне поле в зазорі розглядається як плоськопараллельноє;
2. якір приймається гладким; не враховується спотворення поля; крива поля вважається синусоїдальною; магнітна вісь обмотки збудження співпадає з подовжньою віссю машини;
3. магнітні осі фазних обмоток зрушені на 120°; нехтують полями вищих гармонійних і моментами від цих полів;
4. розподіл струмів в демпферній обмотці синусоїдальний;
5. не враховується вплив вихрових струмів і гістерезису;
6. не враховується вплив насичення.
7. фазні обмотки мають рівні параметри.
Не дивлячись на ідеальність, насправді, із-за спеціальної форми полюсного наконечника і так як СМ працює, як правило, на вигині характеристики холостого ходу, відхилення від синусоїдальності не перевищує 5%.
При складанні СДУ всі параметри зазвичай приводить до системи відносних одиниць (о.е.), яка аналогічна системі о.е. АД, необхідно тільки додати:
- відносне значення опору обмотки збудження
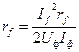
- інерційна постійна
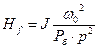
Рівняння якірного ланцюга машини
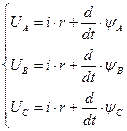
Рівняння ланцюга збудження
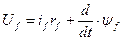
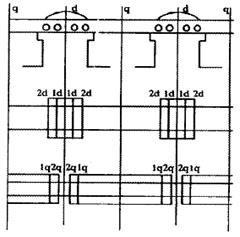
Демпферна обмотка представляється у вигляді окремих контурів, розташованих по двох осях симетрії машини.
Для подовжньої осі машини 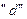 :
:
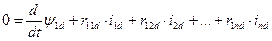 ;
;
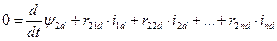 ;
;
……………………………...............
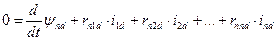 ;
;
Для поперечної осі:
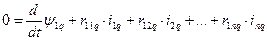 ;
;
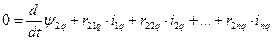 ;
;
……………………………………..
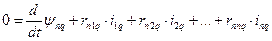 ,
,
де 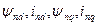 - відповідно потокосцепленіє і струм n–го демпферного контура в подовжній і поперечній осі;
- відповідно потокосцепленіє і струм n–го демпферного контура в подовжній і поперечній осі; 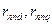 активний опір n-го контура струму цього контура в подовжній і поперечній осі;
активний опір n-го контура струму цього контура в подовжній і поперечній осі; 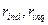 - активний опір i-го контура струму n–го контура.
- активний опір i-го контура струму n–го контура.
Рівняння для потокосчеплень:
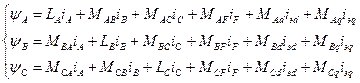
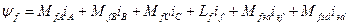 ;
;
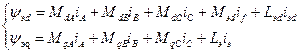
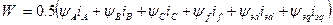 ;
;
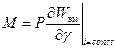 ;
;
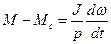 .
.
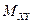 - взаємні індуктивності обмоток Х і Y,L – власна індуктивність; індекси
- взаємні індуктивності обмоток Х і Y,L – власна індуктивність; індекси 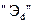 і
і 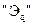 відносяться до демпферних контурів,
відносяться до демпферних контурів, 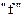 - до обмотки збудження.
- до обмотки збудження.
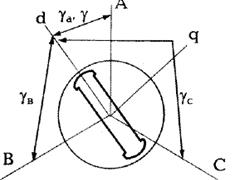
Розглянемо визначення індуктівностей обмоток статора.
Індуктивності обмоток є періодичними функціями кута між магнітною віссю фази і подовжньою віссю 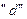 з періодом рівним
з періодом рівним 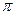 .
.
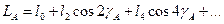
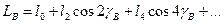
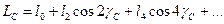
При прийнятій ідеалізації достатньо не більше два доданків
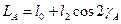
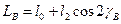
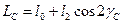
Підставивши значення кутів з малюнка, отримаємо
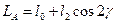
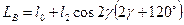
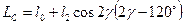
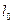 - середньо значення індуктивності фазної обмотки
- середньо значення індуктивності фазної обмотки
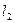 - амплітуда зміни індуктивності.
- амплітуда зміни індуктивності.
У неявнополюсних машинах:
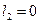 ;
; 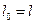 ;
; 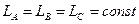
Розглянемо визначення взаємних індуктівностей.
Взаємні індуктивності є парною періодичною функцією кута між віссю "d" і лінією, проведеною між магнітними осями даних фаз.
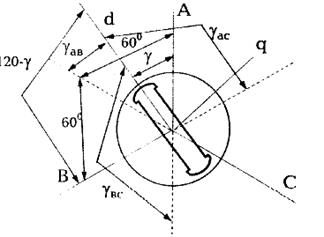
Наприклад, взаємна індуктивність 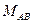 буде парною функцією кута
буде парною функцією кута 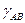
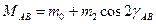
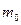 - постійна складова взаємної індуктивності,
- постійна складова взаємної індуктивності, 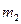 - амплітуда зміни взаємній індуктивності, причому
- амплітуда зміни взаємній індуктивності, причому 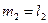
Враховуючи кути
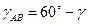
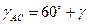
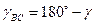
Отримаємо:
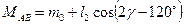
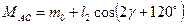
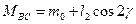
У неявнополюсних 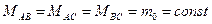
Взаємні індуктивності між фазами і обмоткою збудження
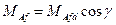
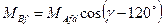
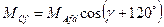
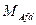 - взаємна індуктивність обмоток при совпаденії їх магнітних осей.
- взаємна індуктивність обмоток при совпаденії їх магнітних осей.
Аналогічно запишемо взаємні індуктивності між фазними обмотками і демпферними контурами для подовжнього контура
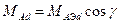
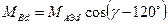
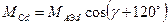
Для поперечного контура
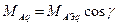
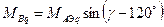
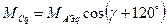
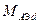 і
і 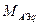 - взаємні індуктивності фазної обмотки і відповідно подовжнього і поперечного демпферного контура при збігу магнітних осей роторного контура і обмотки статора.
- взаємні індуктивності фазної обмотки і відповідно подовжнього і поперечного демпферного контура при збігу магнітних осей роторного контура і обмотки статора.
У практичних розрахунках приймають:
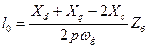
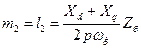
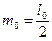
Індуктивність обмотки збудження:
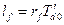
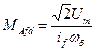
Параметри демпферних контурів:
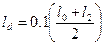 ;
; 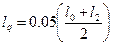
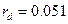 ;
; 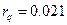
Таким чином, цілий ряд індуктівностей, визначальних потокосчеплення, є періодичною функцією кута 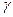 . При обертанні ротора за час dt кут
. При обертанні ротора за час dt кут 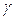
змінюється на 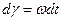
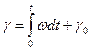
Где 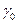 значення
значення 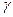 при t=0.
при t=0.
При 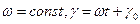
Таким чином, з вищевикладеного можна сформулювати наступні недоліки СДУ у фазних координатах:
1. рівняння електричної рівноваги містять змінні, що є функціями кутового положення ротора;
2. СДУ не представіма в канонічному вигляді;
3. рішення СДУ можливо тільки чисельно з промежуточним рішенням системи рівнянь(аналогічно АД) алгебри.
Ці недоліки досить, щоб зробити завдання моделювання синхронної машини дуже важкої.
В зв'язку з цим застосовують запис СДУ в ортогональній системі координат 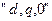 .
.
Дата добавления: 2021-01-11; просмотров: 482;











