Полосы равной толщины
Возьмем пластинку в виде клина. Пусть на нее падает параллельный пучок света. Рассмотрим лучи, отразившиеся от верхней и нижней граней пластинки. Если эти лучи свести линзой в точке 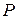 , то они будут интерферировать. При небольшом угле
, то они будут интерферировать. При небольшом угле 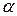 между гранями пластинки, разность хода лучей можно вычислять по форму
между гранями пластинки, разность хода лучей можно вычислять по форму  ле для плоскопараллельной пластинки. Лучи образовавшиеся от падения луча в некоторую другую точку пластинки соберутся линзой в точке
ле для плоскопараллельной пластинки. Лучи образовавшиеся от падения луча в некоторую другую точку пластинки соберутся линзой в точке 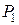 . Разность их хода определится толщиной пластинки в соответствующем месте. Можно доказать, что все точки типа Р лежат в одной плоскости, проходящей через вершину клина.
. Разность их хода определится толщиной пластинки в соответствующем месте. Можно доказать, что все точки типа Р лежат в одной плоскости, проходящей через вершину клина.
Если расположить экран так, чтобы он был сопряжен с поверхностью, в которой лежат точки P, Р1 Р2 то на нем возникнет система светлых и темных полос, каждая из которых образована за счет отражений от пластинки в местах определенной толщины. Поэтому в данном случае полосы называются полосами равной толщины.
При наблюдении в белом свете полосы будут окрашенными. Локализованы полосы равной толщины вблизи поверхности пластинки. При нормальном падении света – на поверхности.
В реальных условиях, при наблюдении окрашивания мыльных и масляных пленок наблюдается полосы смешанного типа.
Дата добавления: 2021-01-11; просмотров: 447;











