Закон равной вероятности.

Если рассеивание размеров зависит только от одного параметра (т. н. Доминирующего фактора, например износа инструмента), то распределение действительных размеров партии обработанных деталей подчиняется закону равной вероятности.

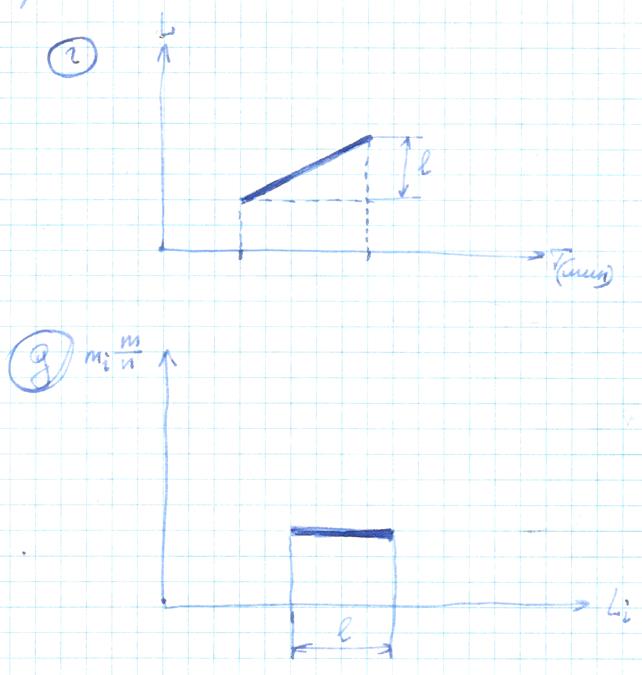
[рисунки «г», «д»]

Так, например, если износ обрабатываемого инструмента, например резца, во времени подчиняется прямолинейному закону (рис. «г»), то действительные размеры обрабатываемых деталей изменяются также строго постоянно, увеличиваясь при обработке валов и уменьшаясь при обработке отверстий, т. к. износ инструмента (резца) даёт изменение длины резца во времени по прямолинейному закону (рис. «г»), то приращение размера обрабатываемых деталей также подчиняется прямолинейному закону (рис. «д»), т. е. закону равной вероятности.

Распределение размеров обрабатываемых деталей также подчиняется закону равных вероятностей при изготовлении с достаточно высокой точностью (порядка 6...7 квалитета и точнее). Фактическое рассеивание в этом случае может быть определено из выражения:

Δ = (2√3)σ

Закон Симпсона.

При наличии больших погрешностей обработки, связанных с недостаточной жёсткостю системы СПИД, износа режущего инструмента и других причин, т. е. когда доминирующих погрешностей 2 или 3, фактическое распределение действительных размеров подчиняется закону Симпсона, известного также под названием закона треугольника.

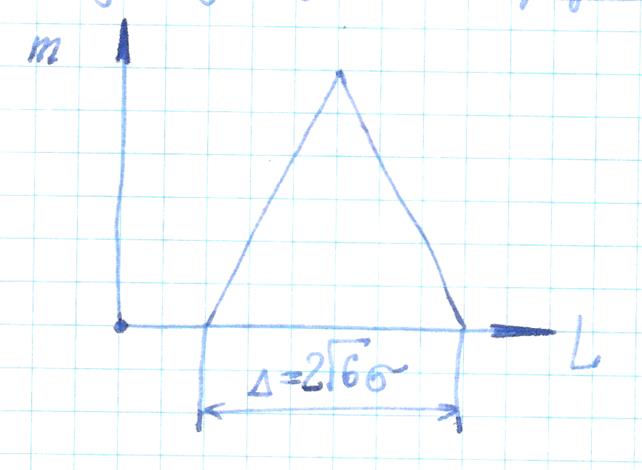
Распределение действительных размеров деталей по закону Симпсона встречается при более грубой обработке (по 9...10 квалитету и грубее). Фактическое поле рассеивания размеров в этому случае:

Δ = (2√6)σ