Практические аспекты кригинга
Содержание
Эта глава дает обзор практических аспектов кригинга: отрицательные веса кригинга, влияние выбранной модели вариограммы на веса кригинга, перекрестная проверка, экранный эффект и некоторые критерии для проверки качества кригинга.
Введение
Эта глава рассматривает практические аспекты кригинга. Представлены некоторые теоретические результаты (например, идея об отрицательных весах кригинга), но глава имеет скорее практический характер. Большинство приводимых концепций рассматриваются на конкретных примерах.
Первый параграф посвящен отрицательным весам кригинга, которые могут привести к отрицательным кригинговым оценкам. Двумя обычными ситуациями появления отрицательных весов могут быть случаи, когда точки сгруппированы (кластеризованы) или, когда используется высоко структурированная модель вариограммы (например, гауссовская модель без эффекта самородков или степенная модель с порядком больше чем 1.0). Для обоих случаев представлены примеры.
Во второй части параграфа обсуждается влияние модели вариограммы на кригинг. Показана форма вариограммы около начала, которая является критической. Вариограммы с различными пропорциями эффекта самородка (т.е. - процента от величины порога) или с различными формами графика в начале (линейная или квадратичная) приводят к весьма разным весам кригинга и дисперсии кригинга, и, следовательно, к различным сортовым планам, построенным на основе кригинговых расчетов. Утверждая это, важно обратить внимание на то, что совмещаемые модели порождают (фактически) одинаковые кригинг системы и, следовательно, подобные веса кригинга и дисперсии кригинга. Поэтому в данном случае кригинг достаточно устойчив относительно незначительных различий в моделях вариограмм.
Третий параграф имеет дело с экранным эффектом. Когда модель вариограммы имеет хорошую структуру (большую зону, малый эффект самородка), информация около целевой точки эффективно экранирует влияние более отдаленных данных. Веса кригинга удаленных точек - нулевые или незначительны. Однако для моделей с плохой структурой экранный эффект - "рассеивается", и тогда требуется больший размер окрестности кригинга. Увеличение размера окрестности ведет к снижению дисперсии кригинга и к существенному улучшению оценки.
Четвертый параграф посвящен симметрии в конфигурации кригинга. На практике данные часто расположены по регулярной сетке. Если используется симметричное расположение данных относительно целевой точки, то некоторые из весов будут равными. Обнаружение этого позволяет геостатистикам перегруппировать множества весов кригинга и, таким образом, сократить размер кригинг системы, а следовательно - требуемое время работы компьютера.
Пятый параграф представляет некоторые критерии для проверки качества конфигурации кригинга. Наиболее очевидный критерий - дисперсия кригинга часто оказывается относительно нечувствительным. Два других параметра: вес среднего в простом кригинге и наклон линейной регрессии являются более полезными, особенно при выборе размера окрестности кригинга.
Последний параграф посвящен обращается вопросу перекрестной проверки моделей вариограмм. Точки одна за другой удаляются из начальных данных. Отсутствующая точка оценивается кригингом. Если модель вариограммы хорошо согласуется с данными, то кригинг оценки должны быть близки к истинным значениям. Обсуждается несколько статистик для количественного определения близости оценок и реальных значений
Отрицательные веса
Важно понять, что дисперсия кригинга не может быть отрицательной, а веса кригинга могут быть. (Отрицательная дисперсия кригинга может быть результатом использования модели вариограммы, которая не определенна положительно, или результатом ошибки программы, например, при дискретизации блоков). Следующий пример продемонстрирует два простых случая, когда возникают отрицательные веса. Первый - рассматривает две вариограммы с очень хорошей структурой (гауссова и степенная модели с показателем степени 1.5), а второй посвящен кластеризации точек.
Пример 1. Предполагается, что пробы были взяты в четырех точках P1, P2, P3 и P4, которые расположены регулярно на расстоянии 1м вдоль линии. Оценивается значение срединной точки P0. Расположение точек показано на Рис. 8.1.
P1 P2 P0 P3 P4
 * * * * *
* * * * *
Рис 8.1. Расположение четырех проб P1, P2, P3 и P4 и целевой точки P0
Для сравнительных целей для кригинга точки использовалось четыре модели вариограмм. Это:
модель степенной функции с показателем степени 1.5 (т.е. 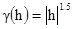 ),
),
гауссова структура с параметром расстояния a=0.8 и порогом 1.0 без эффекта самородка,
гауссова структура с параметром расстояния a=0.8, порогом 0.75 и эффектом самородка 0.25 (т.е. полный порог равен 1.0) и
сферическая модель с зоной 1.38 без эффекта самородка.
Практическая зона гауссовой структуры равна 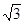 ее реальной зоны; здесь - 1.38. Сферическая модель имеет такую же зону, но она линейна в начале, а не квадратичная. В Таблице 8.1 приведены веса кригинга, соответствующие этим вариограммам. В силу симметричности веса для P2 и P3 одинаковы (l2), также как и для P1 и P4 (l1) .
ее реальной зоны; здесь - 1.38. Сферическая модель имеет такую же зону, но она линейна в начале, а не квадратичная. В Таблице 8.1 приведены веса кригинга, соответствующие этим вариограммам. В силу симметричности веса для P2 и P3 одинаковы (l2), также как и для P1 и P4 (l1) .
Таблица 8.1. Веса кригинга, соответствующие четырем моделям вариограмм. Нумерация весов такая же, как на Рис. 8.1.
| Веса кригинга | Степенная модель 1.5 | Гауссова + эф. самород. | Гауссова без эф. самород. | Сферическая без эф. Самород. |
| l1 | -0.047 | -0.083 | 0.008 | 0.010 |
| l2 | 0.547 | 0.583 | 0.492 | 0.490 |
| Дисперсия кригинга | 0.201 | 0.227 | 0.563 | 0.590 |
Для первых дух моделей веса внешних точек отрицательны (степенная модель cо степенью 1.5 и гауссова без эффекта самородка), потому что они являются моделями с высокой структурой. В отличие от них последние две модели (гауссова с эффекта самородка 25 % и сферическая) имеют менее хорошую структуру и, следовательно, не дают отрицательных весов. При выборе модели вариограммы важно понять, что модель, которая является квадратичной в начале (особенно без эффекта самородка) соответствует более структурированному явлению, чем модель, которая является линейной в начале. Следовательно, более вероятно, что она вызовет отрицательные веса и, следовательно, отрицательные значения кригинга (которые не желательны в горной промышленности).
Пример 2. В этом примере мы обсуждаем влияние кластеризации точек. Близко расположенные точки могут помочь в оценивании поведения вариограммы около начала, но они могут стать причиной численной неустойчивости при обращении матрицы кригинга.
Предполагается, что мы хотим оценить квадрат 100м на 100м по 5 пробами, по одной в каждом углу блока и одна в центре блока. Пусть вариограмма будет сферической с зоной 200м и порогом 2.0. Обратите внимание, что эта модель линейна в начале и, поэтому менее вероятно появление отрицательных весов кригинга, чем для гауссовой, кубической или степенной модели с показателем степени, большим чем 1.0.
(-50,50) (50,50)
· 

 *
*
*(0,0)
(-50,-50) (50,-50)
·  *
*
*
(51,51)
Рис 8.2. Расположение точек проб относительно оцениваемого блока
В Таблице 8.2 даны кригинг веса для конфигурации данных из 5 и 6 точек. Так как отсутствует эффект самородка, веса кригинга для 4 точек изменяются очень слабо от конфигурации из 5 точек к конфигурации из 6 точек. Сумма весов для пятой и шестой точек (грубо) равна пятому весу в конфигурации из 5 точек. Шестая точка получает отрицательный вес. Дисперсия кригинга в этом случае также мало отличается для конфигураций из 5 и из 6 точек. Поэтому мы видим, что для структур без эффекта самородка результаты для 6 точек очень близки к результатам, полученным перегруппировкой последних двух точек. Преимущество перегруппировки точек заключается в том, что она позволяет избежать дополнительного ряда и колонки в матрице, которые иногда могут приводить к числовой нестабильности.
Таблица 8.2. Веса кригинга и дисперсия кригинга для сферической модели и конфигураций из 5 и 6 точек проб
| Веса кригинга | 5 точек | 6 точек |
| (0,0) | 0.43() | 0.436 |
| (-5(),-50) | 0.141 | 0.141 |
| (-50,50) | 0.141 | 0.141 |
| (50,-50) | 0.141 | 0.141 |
| (50,50) | 0.141 | 0.152 |
| (51,51) | - | -0.011 |
| Дисперсия кригинга | 0.085 | 0.085 |
Результаты были бы другими, если бы присутствовал значительный эффект самородка. Веса были бы распространены более равномерно по всем доступным точкам данных. Добавление дополнительной точки также привело бы к заметному снижению дисперсии кригинга.
Эти простые примеры показывают два случая, когда возникают отрицательные веса: когда модель высоко структурирована (например, квадратичная в начале) и, когда присутствует сгущение (кластеризация) точек. Мы видим, что, если выбрана менее структурированная модель, типа сферической, или, когда присутствует эффект самородка, отрицательные веса имеют тенденцию исчезать или, по крайней мере, уменьшаться. Кто хочет найти больше информации об этом, может обратиться к Barnes (1984) и Chauvet (1988).
Дата добавления: 2019-05-21; просмотров: 905;











