Дисперсия точечной пробы внутри объема

Сейчас рассмотрим, как оценить дисперсию блоков по вариограмме проб. Обозначим основания с разными объемами, как v (меньшее) и V(большее). Если данные двухмерные, то это будут области, а не объемы. В нашей модели изучаемые переменные предполагаются, как реализации z(x) случайной функции Z(x). Если все значения величины внутри объема V доступны, то можно найти среднее содержание и дисперсию внутри этого объема. Среднее равно

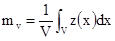[6.1]

а дисперсия содержаний внутри объема V

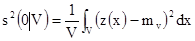[6.2]

Здесь 0 означает точку с практически нулевым объемом. Если мы рассмотрим разнообразие реализаций, то дисперсию z(x) внутри V можно получить, как математическое ожидание 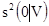для всех возможных реализаций:

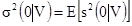6.3]

Можно показать, что эта дисперсия связана с вариограммой формулой:

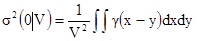[6.4]

Этот интеграл есть среднее, вычисленное изменением x и y независимо по всему объему V. Поэтому введем обозначение 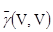. Получим

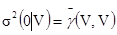[6.5]

На практике 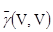вычисляется дискретизацией блока V. Упражнение 6.1 в конце главы покажет читателю, как производятся такие вычисления.