Связь изменчивости с размером блока

Чтобы проиллюстрировать эффект основания, мы вернемся к данным примера, рассмотренного в Главе 1. В Таблице 6.1 приведены содержания 64 блоков 1*1м, а также содержания для шестнадцати блоков 2*2м, каждое из которых представляет собой среднее содержание для 4-х смежных блоков размером 1*1м. Эти величины получены из 1000 анализов, изученных Sandjivy (1980). Как и ожидалось, средние обеих множеств практически одинаковы (201). Небольшая разница обусловлена округлениями содержаний до целых чисел.. Но дисперсии множеств не одинаковы. Дисперсия для блоков 2*2м равна 16,641, что значительно меньше, чем для блоков 1*1м (27,592). Если данные статистически независимы, то дисперсия для большего основания будет составлять 25% от меньшего. Поскольку в данном случае множества коррелируют между собой, то разница получается меньше.

Рис. 6.1 и 6.2 показывают, что формы гистограмм тоже изменяются. Вторая гистограмма менее асимметрична. Выводы этого исследования очень важны для горного дела. При селективной добыче выгодно добывать только те блоки, содержание в которых выше бортового. Поэтому очень важно как можно точнее предсказать количество балансовой руды в отрабатываемом месторождении. Как было показано в Главе 1, где для оценивания запасов использовался полигональный метод (метод многоугольника), содержание пробы, попавшей внутрь многоугольника, распространяется на весь объем многоугольника. Это приводит к приравниванию гистограммы содержаний в керновых пробах к гистограмме содержаний в блоках, и, следовательно, к серьезным ошибкам в оценивании извлекаемых запасов, потому что эти гистограммы существенно отличаются, как можно увидеть из Рис. 6.1 и 6.2.

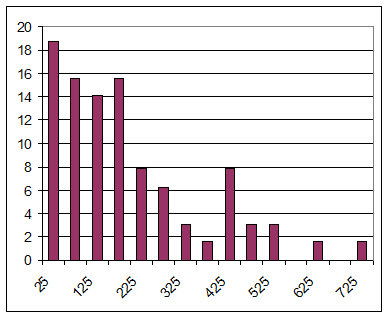
Рис 6.1. Гистограмма содержания 64-х блоков 1м на 1м

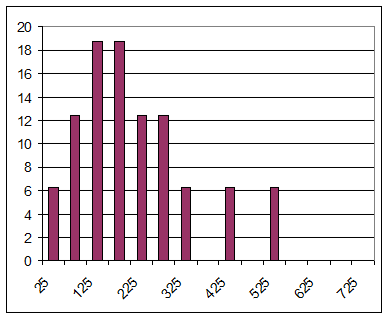
Рис 6.2. Гистограмма содержания 16-ти блоков 2м на 2м

Таблица 6.1. Содержание в (a) шестидесяти четырех блоках 1м на 1м и (b) - в шестнадцати блоках 2м на 2м

а

б