Полная энергия. Закон сохранения полной энергии
Полной энергией системы называется сумма её механической и внутренней энергий:  .
.
Замкнутой (изолированной) называется термодинамическая система, которая не обменивается энергией ни в какой форме с внешней средой.
Для такой системы справедливо: 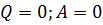 , тогда из первого закона термодинамики следует:
, тогда из первого закона термодинамики следует: 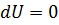 , следовательно
, следовательно 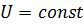 .
.
Если в замкнутой системе 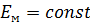 и
и 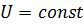 , то
, то 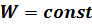 .
.
Полная энергия изолированной системы остаётся неизменной при любых процессах, в ней происходящих.
Понятие изолированной системы – идеализация, все реальные системы незамкнуты.
Теплоёмкость
Для характеристики тепловых свойств тел в термодинамике используют понятие теплоёмкости.
Теплоёмкостью тела называется отношение бесконечно малого количества теплоты, полученного телом в рассматриваемом термодинамическом процессе, к соответствующему приращению его температуры: 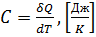 .
.
Значение теплоёмкости 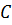 зависит от массы тела, его химического состава, термодинамического состояния и процесса, в котором сообщается теплота
зависит от массы тела, его химического состава, термодинамического состояния и процесса, в котором сообщается теплота 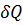 .
.
Удельной теплоёмкостью 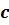 называется теплоёмкость единицы массы вещества:
называется теплоёмкость единицы массы вещества: 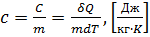 .
.
Удельная теплоёмкость не зависит от массы вещества.
Молярной (мольной) теплоёмкостью называется теплоёмкость одного моля вещества: 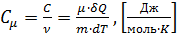 .
.
Теплоёмкость в изохорном и изобарном процессах идеального газа
Для газов различают теплоёмкости при постоянном объёме (в изохорном процессе) 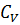 и при постоянном давлении (в изобарном процессе)
и при постоянном давлении (в изобарном процессе) 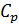 .
.
1). Молярная теплоёмкость идеального газа при постоянном объёме 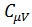
Первый закон термодинамики:
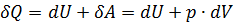 . (1)
. (1)
Молярная теплоёмкость газа: 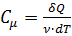 . Для одного моля газа
. Для одного моля газа 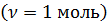 :
:  , следовательно,
, следовательно,
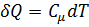 . (2)
. (2)
Из формул (1) и (2) для моля газа следует:
 . (3)
. (3)
В случае идеального газа при 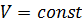 работа внешних сил равна нулю
работа внешних сил равна нулю  и сообщаемое газу извне тепло идёт только на увеличение его внутренней энергии:
и сообщаемое газу извне тепло идёт только на увеличение его внутренней энергии:
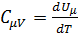 . (4)
. (4)
Для моля идеального газа:
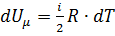 . (5)
. (5)
Тогда из формул (4) и (5) следует: 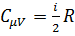
2). Молярная теплоёмкость идеального газа при постоянном давлении 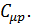 Уравнение Майера
Уравнение Майера
Если газ нагревается при постоянном давлении 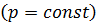 , то уравнение первого закона термодинамики можно представить в виде:
, то уравнение первого закона термодинамики можно представить в виде:
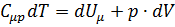
или 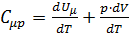 , где
, где 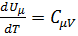 .
.
В итоге получим:
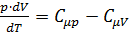 . (6)
. (6)
Уравнение Клапейрона – Менделеева для моля идеального газа 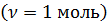 :
: 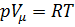 . Продифференцируем последнее выражение по температуре:
. Продифференцируем последнее выражение по температуре: 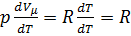 , где
, где 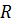 – универсальная газовая постоянная.
– универсальная газовая постоянная.
С учётом последнего выражени уравнение (6) можно представить в виде: 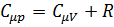 . Последнее уравнение называется уравнением Майера.
. Последнее уравнение называется уравнением Майера.
В окончательном виде уравнение Майера:
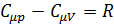 ;
;
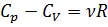 ;
;
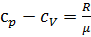 .
.
Как видно из уравнения Майера всегда 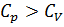 , т.к. при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
, т.к. при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
Из предудущих уравнений и уравнения Майера следует:
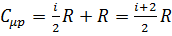 ,
,
т.е.
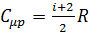 .
.
При рассмотрении термодинамических процессов важно знать характерное для каждого газа соотношения: 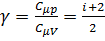 , называемое коэффициентом Пуассона или показателем адиабаты.
, называемое коэффициентом Пуассона или показателем адиабаты.
Для различных газов этот показатель имеет следующие значения:
- для одноатомного газа 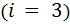 :
: 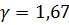 ;
;
- для двухатомного газа 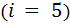 :
: 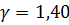 ;
;
- для трёхатомного и многоатомного газа 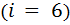 :
: 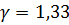 .
.
Закон равномерного распределения энергии идеального газа по степеням свободы молекул приводит к выводу, что теплоёмкости газов зависят от числа степеней свободы молекул и не зависят от температуры. Экспериментальные данные опровергают этот вывод классической теории теплоёмкости: с увеличением температуры теплоёмкость газов возрастает, а с понижением температуры – убывает. Объяснение этого дано в квантовой теории теплоёмкостей.
Теплоёмкость твёрдых тел. Правило Дюлонга и Пти
Для твёрдых тел не различают теплоёмкости 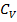 и
и 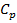 . Основной вклад в теплоёмкости неметаллических твёрдых тел вносит энергия тепловых колебаний частиц, находящихся в узлах кристаллических решёток. Для неметаллов незначительный вклад в теплоёмкость вносит вырожденный электронный газ[40].
. Основной вклад в теплоёмкости неметаллических твёрдых тел вносит энергия тепловых колебаний частиц, находящихся в узлах кристаллических решёток. Для неметаллов незначительный вклад в теплоёмкость вносит вырожденный электронный газ[40].
В основе классической теории теплоёмкости твёрдых тел лежит закон равномерного распределения энергии по степеням свободы. Однородное твёрдое тело рассматривается как система независимых друг от друга частиц, имеющих 3 степени свободы и совершающих колебания с одинаковой частотой. Средняя энергия, приходящаяся на одну степень свободы 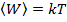 . Внутренняя энергия моля твёрдого тела:
. Внутренняя энергия моля твёрдого тела:
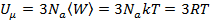 ,
,
где 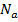 – постоянная Авогадро,
– постоянная Авогадро, 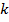 – постоянная Больцмана,
– постоянная Больцмана, 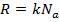 – универсальная газовая постоянная.
– универсальная газовая постоянная.
Молярная теплоёмкость твёрдого тела с атомной кристаллической решёткой:
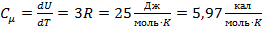 .
.
Правило Дюлонга и Пти: Молярная теплоёмкость всех химически простых кристаллических твёрдых тел приблизительно равна 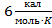 .
.
Согласно этому правилу молярная теплоёмкость твёрдых тел не должна зависеть от температуры, ни от каких-либо характеристик кристаллов. Опыты опровергают это и указывают на зависимость теплоёмкости от температуры, в особенности в области низких температур. Причины расхождения с опытом классической теории теплоёмкости твёрдых тел состоят в ограниченности использования закона равномерного распределения энергии по степеням свободы и непригодности его в области низких температур, где среднюю энергию колеблющихся частиц в кристаллической решетке необходимо вычислять по законам квантовой механики.
Дата добавления: 2016-09-26; просмотров: 1888;











