Применение первого закона термодинамики к изопроцессам идеального газа
С учётом того, что 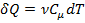 и
и 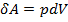 , первый закон термодинамики можно представить в виде:
, первый закон термодинамики можно представить в виде: 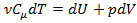 .
.
Изобарный процесс 
Первый закон термодинамики для изобарного процесса имеет вид:
 ,
,
где 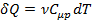 ;
; 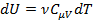 ;
; 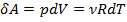 .
.
Из последнего равенства следует: 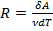 , т.е.
, т.е. 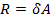 при
при 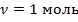 и
и  , т.е. универсальная газовая поcтоянная R численно равна работе, совершаемой одним молем идеального газа при нагревании его на один градус.
, т.е. универсальная газовая поcтоянная R численно равна работе, совершаемой одним молем идеального газа при нагревании его на один градус.
Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе:
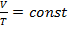 .
.
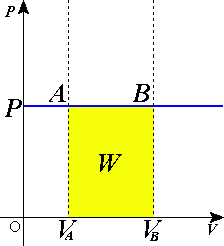 Рис. 123.
Рис. 123.
|
График изобарического расширения газа от объёма
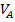 до
до 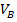 ,
, 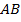 здесь является изобарой, изображён на рис. 123.
здесь является изобарой, изображён на рис. 123.
Изохорный процесс 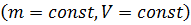
Так как в изохорном процессе 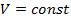 , следовательно
, следовательно 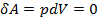 ,
,
т.е. в изохорном процессе работа не совершается.
Первый закон термодинамики для изохорного процесса : 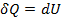 ,
,
т.е. всё количество теплоты, подводимое к газу идёт на изменение его внутренней энергии,где 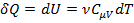 .
.
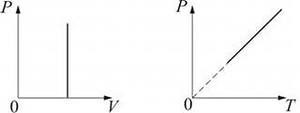 Рис. 124.
Рис. 124.
|
Математически изохорный процесс описывается уравнением Шарля:
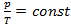 .
.
График изохорного процесса – изохора (рис. 124).
Изотермический процесс 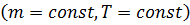
Так как при изотермическом процессе 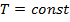 , то изменение внутренней энергии
, то изменение внутренней энергии 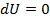 , т.е. внутренняя энергия системы
, т.е. внутренняя энергия системы 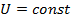 .
.
Первый закон термодинамики для изотермического процесс: 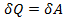 ,
,
т.е. всё количество теплоты, сообщаемое газу, расходуется на совершение работы против внешних сил.
Для конечного процесса: 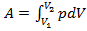 .
.
Т.к. согласно уравнению Менделеева – Клапейрона: 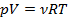 , следовательно,
, следовательно, 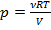 . Таким образом,
. Таким образом, 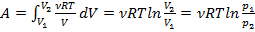 .
.
То есть: 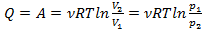 .
.
Чтобы при работе расширения температура не уменьшалась, к газу в течении изотермического процесса необходимо подводить количество теплоты, эквивалентное работе расширения.
Уравнением изотермического процесса является уравнение Бойля- Мариотта:
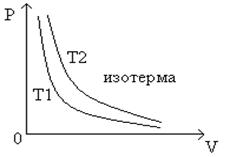 Рис. 125.
Рис. 125.
|
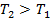
|
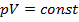 .
.
Графиком изотермического процесса является гипербола – изотерма (рис. 125):
2.10. Применение первого закона термодинамики к адиабатному процессу 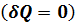
Так как в адиабатном процессе отсутствует теплообмен с внешней средой 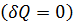 , то первый закон термодинамики для адиабатного процесса имеет вид:
, то первый закон термодинамики для адиабатного процесса имеет вид:
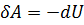 ,
,
т.е. при адиабатном процессе работа совершается за счёт убыли внутренней энергии системы, где 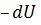 – убыль внутренней энергии системы.
– убыль внутренней энергии системы.
Тогда: 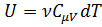 и, соответственно:
и, соответственно:
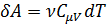 . (1)
. (1)
При адиабатическом расширении газ охлаждается ( 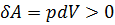 , а
, а 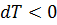 ); при адиабатическом сжатии газ нагревается (
); при адиабатическом сжатии газ нагревается ( 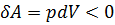 , а
, а 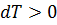 ).
).
Найдём связь между параметрами состояния идеального газа 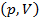 в адиабатном процессе.
в адиабатном процессе.
Представим (1) в виде: 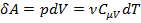 .
.
Из уравнения Клапейрона – Менделеева следует :для изобарного процесса: 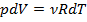 ;для произвольного процесса:
;для произвольного процесса: 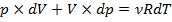 .
.
Таким образом, 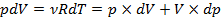 .
.
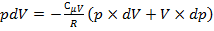 .
.
Так как, согласно уравнению Майера: 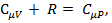 то
то 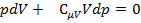
Разделим последнее выражение на 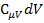 , тогда:
, тогда:  , где
, где 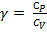 .
.
Так как, 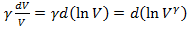 и
и 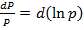 , то уравнение можно представить в виде:
, то уравнение можно представить в виде: 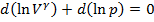 или
или 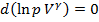
Таким образом, в равновесном адиабатном процессе изменение состояния идеального газа описывается уравнением Пуассона (уравнением адиабаты):
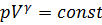 .
.
Последнее уравнение можно записать также в виде:
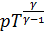 или
или 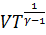 .
.
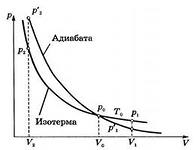 Рис. 126.
Рис. 126.
|
На диаграмме в координатах
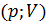 адиабата имеет вид гиперболы (рис. 126):
адиабата имеет вид гиперболы (рис. 126):
Адиабата идёт круче изотермы. При адиабатном сжатии увеличение давления обусловлено не только уменьшением объёма газа, как при изотермическом сжатии, но и увеличением температуры. При адиабатном расширении температура газа уменьшается, поэтому давление падает быстрее, чем при изотермическом расширении.
Работа: 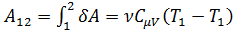 .
.
Из уравнения Майера и соотношения 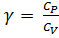 , следует:
, следует: 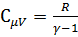 .
.
Поэтому, 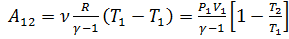 .
.
Из уравнения адиабаты следует: 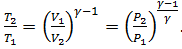
Тогда: 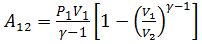 или
или 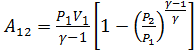 .
.
Графически работа численно равна площади криволинейной трапеции 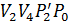
Работа адиабатного расширения 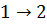 меньше, чем при изотермическом процессе. При адиабатном расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается за счёт притока извне эквивалентного количества теплоты.
меньше, чем при изотермическом процессе. При адиабатном расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается за счёт притока извне эквивалентного количества теплоты.
Дата добавления: 2016-09-26; просмотров: 2642;











