Истечение жидкости из сосуда

Вычислим скорость истечения жидкости через отверстие в сосуде (рис. 11.7). Выделим в толще жидкости трубку тока. При этом не важна конфигурация этой трубки, важно, что одно её сечение расположено на поверхности жидкости в сосуде, другое — на срезе отверстия. Обе эти поверхности находятся под одним и тем же статическим атмосферным давлением — Р₀. Гидростатические давления в сечениях будут определяться высотами h₀ и h. Задав скорости жидкости в сечениях V₀ и V, запишем на основании уравнения Бернулли следующее равенство:

,

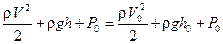или

.

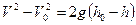Отсюда — искомая скорость истечения:

.

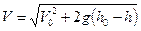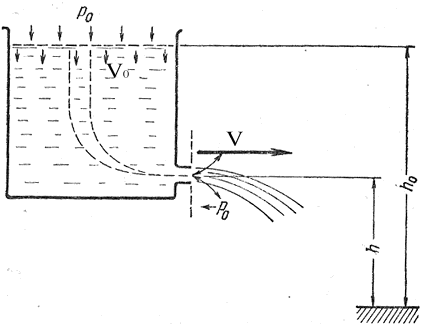
Рис. 11.7

Для отыскания скорости V₀ на свободной поверхности жидкости, воспользуемся уравнением неразрывности:

V₀S₀ = VS.

Если S << S₀, то V₀ = 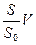— ничтожно по сравнению с V. Поэтому, если сечение отверстия S много меньше площади открытой поверхности жидкости в сосуде S₀, то последнее уравнение можно упростить:

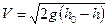. (11.9)

Это известная формула Торричелли. Согласно этой формуле, скорость истечения идеальной жидкости из отверстия в точности равна скорости, которую приобретает тело, свободно падая с высоты (h₀ – h). Причём эта скорость не зависит от угла к горизонту, под которым вытекает жидкость.

Записав формулу Торричелли по-другому:

,

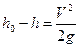приходим к выводу, что если вытекающую струю направить вертикально, то жидкость в идеале поднимется на высоту Dh = h₀ – h, то есть достигнет первоначального уровня h₀.