Гармонический осциллятор.
В классической физике гармоническим осциллятором называют частицу, совершающую движения по закону синуса или косинуса. Потенциальная энергия такой частицы U = кх2/2, частота колебаний 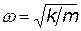 . Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.
. Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.
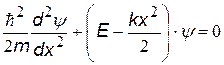
| уравнение Шрёдингера для гармонического осциллятора Т.к. случай одномерный, оператор Лапласа Dy =d2y / dx2, потенциальная энергияU = кх2/2. |
Мы не приводим решение этого уравнения, т.к. оно выходит далеко за рамки курса. Из решения следует, что полная энергия Е такого осциллятора квантуется:

| Полная энергия квантового осциллятора n = 0, 1, 2,…,¥ |
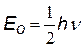 при
n = 0 при
n = 0
| Эта величина называется нулевой энергией осциллятора. |
 По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;
По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;
даже при абсолютном нуле (Т= 0 К) частица имеет энергию ¹ 0.
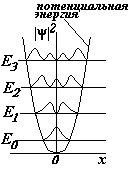
На рис. показаны плотности вероятности 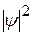 при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.
при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.
Существование нулевой энергии следует также из соотношения неопределенности. Действительно.

| соотношение неопределенностей | |
| Dх » А | неопределенность в координате примем равной амплитуде А колебаний | |
| Dр » р = mv = mw А | неопределенность в импульсе примем равной самому импульсу; максимальная скорость колебаний v = w А | |
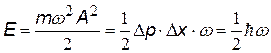
| Е - максимальная энергия гармонических колебаний (Е =кх2/2, 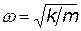 ) )
| |
Таким образом, из соотношения неопределенностей следует, что энергия осциллятора равна 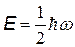 .
.
Дата добавления: 2021-02-19; просмотров: 596;











