Основной закон динамики для идеальной жидкости. Уравнение Бернулли

При течении жидкости между её отдельными частицами возникают силы вязкого сопротивления. В газах эти силы сравнительно невелики, и ими можно пренебречь. Однако и во многих случаях течения жидкости влияние её вязкости так же оказывается несущественным. Идеальной называется жидкость, в которой при любых движениях не возникают силы внутреннего трения (вязкости).

Выделим в стационарном потоке идеальной жидкости элементарный объём dV = dx × dy × dz в виде кубика в точке 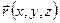(рис. 11.5). Рассмотрим силы, действующие со стороны окружающей жидкости на каждую грань кубика. Эти силы определяют движение выделенного элемента жидкости. В направлении z действуют силы давления

F_z = 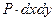и F_(z+dz) = 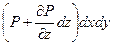и сила тяжести F_T = r_жgdV = r_жgdxdydz.

Рис. 11.5

Запишем уравнение второго закона Ньютона для движения этого элемента в направлении z:

.

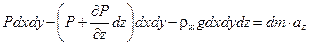Здесь: dm = r_жdxdydz — масса «кубика»;

a_z = — его ускорение в направлении z.

Упростив, получим:

.

Для направлений x и y запишем аналогичные уравнения (без силы тяжести, разумеется):

;

.

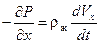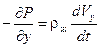Объединим эти скалярные уравнения в одно векторное:

,

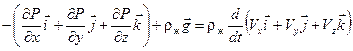или

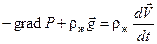. (11.5)

Уравнение (11.5) — основное уравнение динамики идеальной жидкости. В этом уравнении вектор 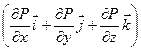называется градиентом давления P и обозначается gradP.

Уравнение Бернулли

Рассмотрим стационарное течение идеальной жидкости. Выделим в потоке трубку тока, а в ней — объём, ограниченный стенками трубки и двумя сечениями S₁ и S₂ (рис. 11.6). Скорости течения в этих сечениях — v₁ и v₂ — соответственно, а сами сечения расположены на уровнях h₁ и h₂. Спустя время Dt выделенные сечения переместятся вместе с жидкостью вдоль линии тока на расстояния Dl₁ = v₁Dt и Dl₂ = v₂Dt. Вычислим изменение энергии выделенного объёма жидкости за промежуток времени Dt:

.

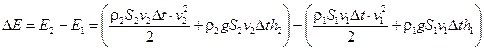Рис. 11.6

Это выражение можно упростить, учитывая, во-первых, несжимаемость жидкости: r₁ = r₂ = r и, во-вторых, уравнение неразрывности потока: S₁v₁Dt = S₂v₂Dt = DV:

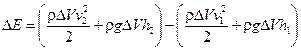. (11.6)

Поскольку сила вязкого сопротивления при этом перемещении отсутствует (жидкость идеальна), найденное изменение энергии обусловлено работой только сил давления А(Р) = Е₂ – Е₁:

A = P₁S₁Dl₁ – P₂S₂Dl₂ = (P₁ – P₂)DV. (11.7)

Приравняв работу сил давления (11.7) изменению механической энергии выделенного элемента трубки тока (11.6), получим:

.

Последнее уравнение принято представлять так:

.

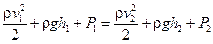Сечения S₁ и S₂ выбраны произвольно, поэтому полученный результат можно трактовать шире: при стационарном течении идеальной жидкости в любом сечении трубки тока выполняется следующее условие:

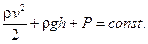(11.8)

Это и есть уравнение Бернулли для стационарного течения идеальной жидкости. В этом уравнении: Р — статическое давление;

rgh — гидростатическое давление;

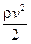— динамическое давление.

Далее на ряде примеров покажем, как используется уравнение Бернулли для решения различных задач гидродинамики.