Устойчивость сжатого стержня. Задача Эйлера

Р

При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила Р приложена строго центрально. Рассматриваемый метод решения основан на том, что при достижении силой Р критического состояния (Р=Р_кр) стержень находится в безразличном состоянии и ему присущи две формы равновесия: прямолинейная и криволинейная (в таких случаях говорят, что происходит ветвление, или бифуркация, равновесных состояний). Для выявления криволинейной формы равновесия достаточно приложить к стержню малую поперечную возмущающую нагрузку Q, которая вызовет малый прогиб. Если
Р < Р_кр, то при удалении Q стержень будет сохранять прямолинейную форму равновесия. Если Р > Р_кр, то равновесие стержня становится неустойчивым и сколь угодно малое возмущение достаточно для того, чтобы возникли большие прогибы. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.

Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой Р. Допустим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:

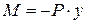, (8.3)

где y – прогиб стержня в произвольном сечении с координатой x.

Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

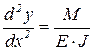, (8.4)

где E – модуль Юнга; J – осевой момент инерции сечения стержня относительно оси z в данном случае; E·J ­– жесткость стержня при изгибе. Знаки левой и правой части согласованны в данной системе координат.

Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = J_min (стержень искривляется относительно оси с наименьшим моментом инерции)

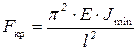(8.5)

Это выражение обычно называют формулой Эйлера, а определяемую с ее помощью критическую силу – эйлеровой силой.