Зависимость критической силы от условий закрепления стержня

Формула Эйлера была получена для основного случая – шарнирного опирания стержня по концам (рис.8.3). На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.

Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.

1. Стержень длиной l закреплен в жесткой заделке и сжат продольной силой (рис.8.4,а). Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев можем сделать вывод, что ось стержня, защемленного одним концом, находится в тех же условиях, как и верхняя половина шарнирно опертого стержня длиной 2·l. Таким образом, критическая сила для стержня длиной l с одним защемленным концом может быть найдена так же, как и для шарнирно опертой балки длиной 2·l, то есть

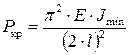. (8.6)

2. Стержень длиной l, у которого оба конца жестко защемлены (рис.8.4,б). Средняя часть стержня, с двумя жестко защемленными концами находится в тех же условиях, что и шарнирно опертая балка длиной l/2. Таким образом, критическая сила для стержня длиной l с двумя защемленными концами может быть определена так же, как и для шарнирно опертой балки длиной l/2, то есть

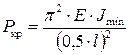. (8.7)

3. Стержень длиной l, у которого один конец жестко заделан, а другой шарнирно оперт (рис.8.4,в). Критическая сила для стержня длиной l с защемленным и шарнирно опертым концами может быть определена так же как и для шарнирно опертой балки длиной 0,7·l, то есть

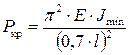. (8.8)

Все полученные решения можно объединить в одну общую формулу

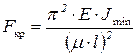, (8.9)

где 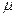·l = l_пр – приведенная длина стержня; l – фактическая длина стержня; 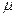– коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: 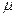показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)

8.4. Критические напряжения. Расчет на устойчивость стержня
при упруго-пластических деформациях

Введем понятие критического напряжения, то есть напряжения, соответствующего критической силе при потере устойчивости сжатого стержня

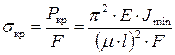. (8.10)

Вспомним, что 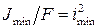– квадрат минимального радиуса инерции. Тогда формулу (8.10) можно записать так:

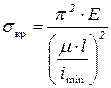(8.11)

Величина

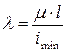(8.12)

называется гибкостью стержня.

Окончательно получим

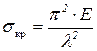(8.13)

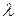Как видим, критическое напряжение зависит только от упругих свойств материала (модуля Юнга E) и гибкости стержня. При этом зависимость между σ_кр и может быть представлена гиперболической кривой, называемой гиперболой Эйлера.

σт σпп

Вывод формулы Эйлера основан на применении дифференциального уравнения упругой линии балки. Поэтому использовать эту формулу можно лишь в том случае, когда деформирование материала протекает в соответствии с законом Гука, то есть пока критическое напряжение не превысит предела пропорциональности (по диаграмме сжатия материала):

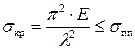(8.14)

Используя это соотношение, можно найти условие для определения предельной гибкости стержня 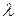_пр, когда еще возможно применение формулы Эйлера:

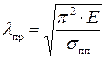(8.15)

Например, для малоуглеродистых сталей (E = 2·10⁵ МПа, 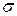_пп ≈
200 МПа) предельная гибкость

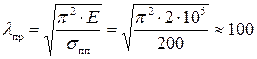(8.16)

Итак, при 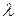> 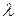_пр для определения критической силы будем пользоваться формулой Эйлера, если же 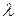< 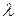_пр, то формула Эйлера становится неприемлемой, так как дает завышенные значения критической силы, то есть всегда переоценивает действительную устойчивость стержней.

Поэтому использование формулы Эйлера для стержней, теряющих устойчивость за пределом пропорциональности не только неправильно, но и опасно.

Теоретическое решение задачи об устойчивости за пределом пропорциональности сложно, поэтому для расчетов на устойчивость в этой области обычно пользуются эмпирическими формулами, полученными в результате обработки большого числа экспериментальных данных.

σпп

Прежде всего, выделим стержни с малой гибкостью, у которых 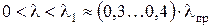(для стали). Эти короткие стержни будут выходить из строя главным образом за счет потери прочности, потеря устойчивости в таких случаях, как правило, не наблюдается. Таким образом, для стержней малой гибкости при сжатии проводят обычный расчет на прочность, принимая в качестве предельного напряжения предел текучести σ_т (для пластичных материалов) или предел прочности σ_в (для хрупких материалов). Этому условию соответствует горизонтальная прямая на рис.8.7.

Для практических (инже-нерных) расчетов стержней средней гибкости, у которых 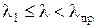чаще всего используется эмпирическая зависимость, предложенная Ф.С. Ясин-ским на основе изучения опытных данных (формула Ясин­ского):

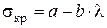, (8.17)

где a и b – эмпирические коэффициенты, зависящие от материала (например, для стали 40: a=321 МПа, b=1,16 МПа).

Формуле Ясинского на диаграмме критических напряжений соответствует наклонная прямая.