Эмпирическая функция распределения и гистограмма результатов испытаний

Чисто технические трудности заставляют нас ограничиться планами [N, U, r] и [N, U, T]. Напомним, что план [N, U, N] означает испытание N изделий до отказа последнего из них; отказавшие изделия не заменяются новыми. План [N, U, N] можно использовать в случае, когда изделия сравнительно ненадёжны, или же при проведении ускоренных испытаний.

Предположим, что испытываемые изделия занумерованы числами 1..N и i-ое изделие отказывает в случайный момент τ_i. Первый отказ наступает в момент t₁=min(τ₁ ,.., τ_N); 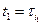, где i₁- номер изделия отказавшего первым; i₁- случайное число. Второй отказ наступает в момент 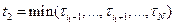, , 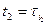i₂ – номер изделия отказавшего вторым и т.д. Наконец, в момент 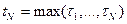отказывает последнее изделие.

В статистике так упорядоченную последовательность чисел t₁ ≤ t₂ ≤ …≤ t_N называют вариационным рядом для результатов наблюдений .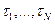

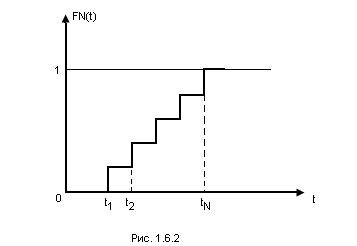
При использовании плана [N, U, T] наблюдаются только те отказы, которые происходят до момента времени T. Если t₁ ≤ t₂ ≤ …≤ t_n(T) ≤ T (отказ с номером n(T)+1, если он возможен, наступает после момента T). Таким образом, n(T) означает номер последнего отказа, который происходит до момента T окончания испытаний. Если изделия достаточно надёжно работают в интервале времени (0, T), то нередко случается, что отказы не наблюдаются и n(T)=0, что, однако не даёт нам права заключать, что надёжность изделий равна единице. Впоследствии мы укажем правило оценки надёжности в подобных случаях, основанное на понятии доверительного интервала. Наиболее полной характеристической надёжности изделий является функция распределения F(t)≡Q(t) для времени безотказной работы. О виде функции F(t) можно судить по так называемой эмпирической функции распределения F_N(t), определяемой равенством:

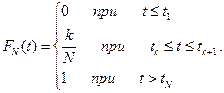(12.1)

Таким образом, эмпирическая функция распределения при каждом значении t случайной величины τ равна числу значений случайной величины, меньших t(числу изделий отказавших до момента t) делённому на общее число испытаний (общем партии N). График функции F_N(t) показан на рис. (12.2.). Если используется план [N, U, T], то значения F_N(t) могут быть определены только для t≤T, т.е. до уровня 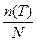. При использовании плана [N, U, r] значения F_N(t) определяются до уровня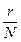

Рис.12.4.

Оценкой плотности вероятности 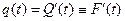может служить гистограмм 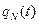. При построении гистограммы строится статический ряд: область значений времени t разбивается на интервалы (разряды) (S_k,S_k+1) k=1,2..m. Целесообразно выбирать m=10–20. На каждом интервале определяется частота 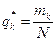, где 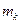-число отказов, которые наблюдаются в интервале (S_k,S_k+1); .

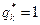Статистическая плотность вероятности на каждом интервале определяется следующим образом:

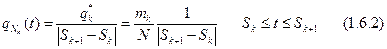
Построение гистограммы иллюстрируется таблицей и рис. 12.3.

Число отказов	m1	m2	...	mk
Ji	S1S2	S2S3	...	SkSk+1
			...
			...

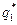
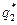
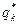
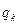
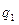
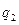
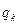
Площадь под гистограммой должна быть равна единице

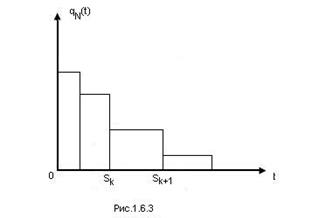
Рис. 12.5.

Статистическая опасность(интенсивность отказов) также можно найти, построив статистический ряд:

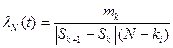, (12.3)

где N-общее число изделий, поставленных на испытания,

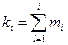- общее число отказов изделий в течение наработки (0, t_i).

Во многих случаях не обязательно знать всю функцию распределения F(t), её плотность вероятности q(t) и функцию опасности отказов λ(t), а достаточно знать лишь некоторые характеристики: моменты, квалитеты и другие характеристики. Используется вариационный ряд.

Начальный момент k-го порядка в случае плана [N, U, N] определяется по формуле:

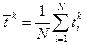. (12.4)

При k=1 имеем статистическое среднее .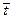

Центральный момент k-го порядка:

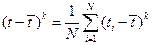. (12.5)

При k=2 формула (12.5) даёт статистическую дисперсию .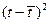

Число t_p такое, что F(t_p)=p, где F(t) функция распределения, называется квантилью уровня “P”. Эмпирической квантилью 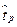уровня “P” называется одно из решений уравнения .

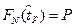Мы всюду предполагаем, что функция F(t) является непрерывной.

Точечные оценки параметров распределения.

Зачастую приходится иметь дело с такой ситуацией, когда нам необходимо на основании испытаний оценить значение одного или нескольких неизвестных параметров. С этой задачей сталкиваются как при нахождении функции распределения, когда известен её аналитический вид, так и при оценке числовых характеристик случайной величины. Одним из наиболее распространённых подходов к оценке параметра является следующий подход. Пусть F(t, α) является функцией распределения случайной величины τ. α – неизвестный параметр (α может быть векторной величиной). Обозначим 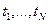результаты независимых испытаний случайной величины τ. Точечной оценкой параметра 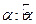будем называть некоторую функцию 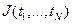, зависящую только от результатов испытаний и известных величин, но не от неизвестного параметра. Оценка является некоторой случайной величиной и поэтому может изменяться от одной серии испытаний к другой. В качестве оценки можно предложить большое число функций J , поэтому, чтобы избежать полного произвола, необходимо наложить на них некоторые естественные условия. Обычно стремятся, чтобы оценки обладали свойствами несмещённости, состоятельности и эффективности. Оценка 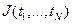параметра α называется несмещённой, если математическое ожидание оценки равно самому параметру, т.е.

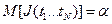. (12.6)

Если нам нужно оценить математическое ожидание случайной величины τ(a=M[τ]), то в качестве оценки можно выбрать функцию

.

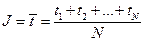Легко подсчитать, что эта оценка является несмещённой.

При оценке параметра 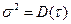посредством эмпирической дисперсии 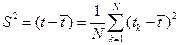получается смещение 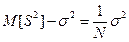. Если мы хотим получить несмещённую оценку 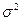, то следует брать функцию .

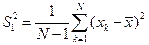Оценка 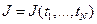параметра α называется состоятельной, если при увеличении числа наблюдений до бесконечности оценка сходится к оцениваемому параметру по вероятности, т.е.

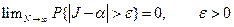(12.7).

Легко проверить, что все приведённые нами выше примеры оценок параметров “α” и 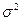являются состоятельными, причём для параметра 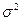состоятельными являются как оценка 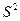, так и оценка 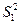. Оценка параметра α является эффективной, если дисперсия оценки не превышает некоторого заданного уровня. Мы скажем, что оценка J₁ эффективнее, чем оценка J₂, если 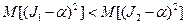. При некоторых общих ограничениях, наложенных на аналитические свойства оценок J, можно указать нижнюю грань для всех оценок рассматриваемого класса: 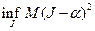. Если оценка 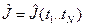такова, что 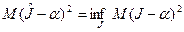, то оценка 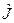называется эффективной. Оценка 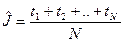для параметра α распределения 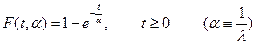эффективна.

Для точной оценки параметров распределений используются: графические методы, метод максимального правдоподобия, методы квантилей и моментов.