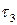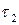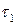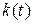Выбор оптимального значения периодичности технического обслуживания

С учетом материала п. 3.4.2. при выборе оптимальной периодичности 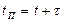технического обслуживания необходимо учитывать двойственный характер требований, предъявляемых к объекту, эксплуатируемому в режиме дежурства, что характерно для многих систем сигнализации и контроля, пожаровзрывопредупреждения и управления, а также для различных транспортных средств, эксплуатируемых в режиме дежурства и применяемых по команде управления и т. д.… Такие объекты в момент поступления команды на применение по назначению, с одной стороны, должны быть в работоспособном состоянии, а с другой стороны, в этот момент они не должны находиться на ТО [2-9].

Вероятность нахождения объекта в работоспособном состоянии в любой момент периода между техническими обслуживаниями оценивается, как это показано в п. 3.4.3, определяется средним значением коэффициента готовности 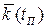, а вероятность нахождения объекта в этот же момент не на техническом обслуживании оценивается с помощью показателя 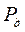, то есть вероятностью .

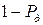С учетом этих соображений в качестве показателя готовности (целевой функции) используется вероятность нахождения ОТС в режиме дежурства, а объекта – в работоспособном состоянии в любой случайный момент 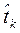поступления заявки (команды) на применение объекта, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается [1].

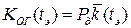, (3.63)

поскольку эта вероятность критична как к изменению вероятности 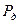нахождения объекта в режиме дежурства, так и к изменению среднего значения коэффициента готовности 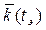. Показатель (3.63) называется коэффициентов оперативной готовности [1-5].

Таким образом, при оптимальном значении периодичности 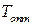проведения ТО должен обеспечиваться баланс между вероятностью нахождения объекта в режиме дежурства и уверенностью в его работоспособном состоянии.

Таким образом, поиск оптимального значения периодичности ТО рассматривается при следующих допущениях:

периодичность и продолжительность ТО постоянны, то есть ;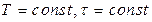

после проведения ТО происходит полное восстановление работоспособности объекта;

время поступления команды на подготовку к применению имеет равномерное распределение в период эксплуатации ;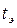

контроль технического состояния объекта в период между ТО отсутствует, поскольку именно с контроля по существу начинается техническое обслуживание.

Для данной модели эксплуатации характер изменения коэффициента готовности во времени приведен на рис. 3.11.

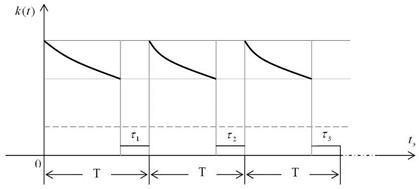
Рис. 3.11 Зависимость коэффициента готовности объекта от периодичности 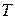технического обслуживания и его длительности .

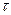Указанная модель применима и для различных встроенных систем контроля. Так, например, при обеспечении работоспособности вычислительных комплексов возникает задача выбора наилучшей (с позиций введения контроля) временной организации системы контроля. При этом предполагается, что длительность выполнения контрольных операций (аналог технического обслуживания) и метод контроля известны. Здесь под временной организацией системы контроля понимается встроенная стратегия включения контролирующий программ, то есть периодичность и последовательность их включения.

Пусть поток отказов (сбоев) в контролируемой вычислительной системе простейший с параметром 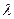, период включения контролирующей программы 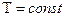, а длительность ее выполнения 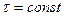, причем отказы, возникшие в системе, выявляются только в процессе работы контролирующей программы. В этом случае максимальную достоверность будет иметь та задача, которая была решена непосредственно после окончания программной проверки. Минимальную достоверность будет иметь решение той задачи, которая решалась непосредственно перед проверкой, что связано с увеличившейся вероятностью 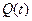использования отказавшей системы при решении этой задачи.

При сделанных предположениях вероятность 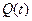использования отказавшей системы является периодической функцией с периодом 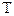, которая изменяется в пределах от 0 до 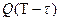. Уменьшение периода контроля 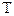повышает достоверность решения задач, но при этом возрастают относительные затраты времени на контроль, определяемые величиной 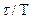, поэтому возникает задача выбора рационального значения периода .

Q(t)

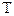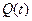Зависимость вероятности использования отказавшего объекта от времени при включении контролирующей программы представлена на рис. 3.12.

Q(t)max

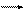
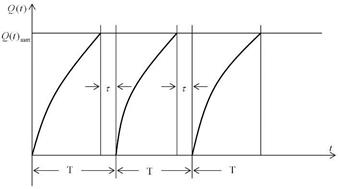
Рис. 3.12 Зависимость вероятности использования отказавшего объекта (вычислительного комплекса) для решения зхадач при включении контролирующей программы на время 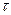с периодичностью .

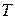В данном случае показатель готовности объекта в соответствии с формулами (3.58), (3.62) определяется следующим образом

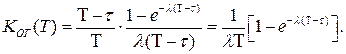(3.64)

Применение формул (3.58), (3.62) для оценки показателя (3.63) в соответствии с моделью, представленной на рис. 3.10, приводит к аналогичному результату

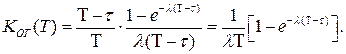. (3.65)

Анализ формул (3.64), (3.65) показывает, что они идентичны и при конечных значениях 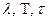функции 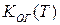имеют максимум при определенном значении T. Действительно, пр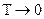и и 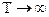выражения (3.64), (3.65) стремятся к нулю, что указывает на наличие максимума функций (3.64), (3.65), достигаемого при некотором оптимальном значении периодичности 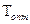восстановления первоначальных свойств контролируемых объектов.

Однако получение 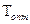представляет значительные трудности, поскольку выражения (3.64), (3.65) являются трансцендентными и допускают решение приближенными методами. С этой целью числитель этих выражений, например (3.65), необходимо разложить в ряд Тэйлора в окрестностях точки 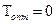, ограничиваясь с достаточной для практики точности первыми тремя членами разложения, что приводит к следующему результату

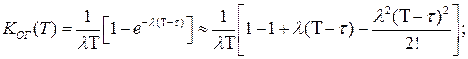
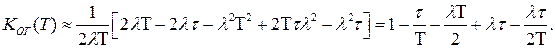(3.66)

Дифференцирование выражения (3.66) приводит к следующему результату

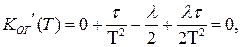
откуда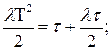

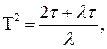
который окончательно принимает следующий вид

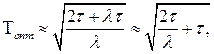
откуда в окончательном виде

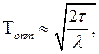(3.67)

поскольку 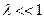. Например, при 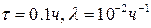, будет иметь место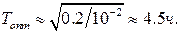

После выбора периода (3.67) включения программы контроля целесообразно определить моменты времени, в которые необходимо начинать программный контроль отдельных компонент объекта.