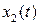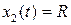Модель отказов, обусловленных накапливающимися повреждениями.

Среди причин возникновения отказов важное место занимает старение объекта, когда отказ объекта образуется за счёт постепенного накопления повреждений (постепенного старения или изнашивания). Следует отметить, что сколь угодно высокое качество объектов не может предохранить их от постепенного старения (износа). Так, в процессе эксплуатации и хранения в металлах, пластмассах и других материалах накапливаются необратимые изменения, которые нарушают прочность (несущую способность или сопротивляемость) объектов и постепенно, в конечном счете, приводят к отказу [14]. Для ряда рабочих параметров объекта заранее могут устанавливаться допустимые пределы, выход за пределы которых квалифицируется как отказ, а время этого выхода является временем безотказной работы.

Модель, когда первое повреждение способно привести к отказу (повреждению) объекта рассмотрена в п.2.1. Модель отказов, обусловленная накапливающимися повреждениями, состоит в том, что для отказа объекта необходимо накопление нескольких повреждений. Таким образом, данная модель является обобщением модели при единичном мгновенном повреждении.

Пусть в случайные моменты времени 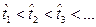возникают единичные случайные повреждения. При накоплении m повреждений возникает отказ. При каждом единичном повреждении износ скачкообразно увеличивается на некоторую случайную величину . На рис. 2.2. приведена схема накопления повреждений при износе, где пунктирная прямая соответствует средней величине износа на интервале [0,t]. 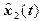Случайные колебания величины износа около этой пунктирной прямой обусловлены случайностью моментов 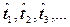возникновения случайных скачкообразных приращений износа .

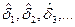Пусть в случайные моменты времени 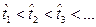возникают единичные повреждения 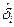, значения которых подчинены закону распределения с математическим ожиданием 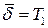, а интервал 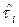между моментами возникновения повреждений подчинён закону распределения с математическим ожиданием .

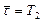На этом этапе стабильный в вероятностном смысле процесс износа приводит к тому, что интервалы 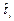, между включениями объекта в рабочее состояние, а также продолжительности или объёмы 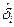работы (величины износа) объекта при каждом таком включении являются случайными величинами с математическими ожиданиями 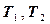и дисперсиями 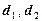соответственно, то есть

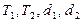. (2.26)

В этом случае износ объекта, то есть сумма 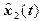накопленых в нём повреждений, образует случайный процесс вида

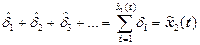, (2.27)

где 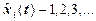- случайное число включений объекта в рабочее состояние за время t.

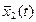На рис. 2.2 с учётом (2.26), (2.27) представлена схема накопления повреждений (износа), где R - сумма повреждений, необходимых для возникновения отказа. Пунктиром показана прямая, описывающая собой среднюю сумму повреждений накопившихся за время t.

Рис. 2.2. Реализация процесса накопления повреждений

Предполагается, что вероятность возникновения скачка износа за время 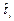не зависит от того, сколько скачков (повреждений) 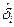было на интервале времени, к которому примыкает этот интервал.

Физический смысл этого предположения заключается в следующем. Процесс износа всегда имеет, по крайней мере, три этапа (рис. 2.3.). На первом этапе (этап I) в процессе приработки в объекте протекают направленные изменения, объект как бы приспосабливается к условиям нагружения. Характерной особенностью этого этапа является взаимная зависимость приращений 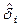износа. Скорость износа на этом этапе постепенно уменьшается вследствие выжигания дефектных. Этап II называется зоной установившегося или нормального износа. На этом этапе объект приобретает относительно стабильные свойства, отвечающие условиям нагружения. Этап нормального износа занимает наибольшую часть времени функционирования (объекта). На II-ом этапе изменения, происходящие в объекте, носят плавно возрастающий характер, поскольку величина приращения износа (числа повреждений) 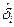не оказывает существенного влияния на величину последующего повреждения [2-5,15,16].

Этап III называется зоной катастрофического износа, поскольку на скорость износа начинают воздействовать появившиеся в ходе износа на втором этапе новые факторы, влияние которых ранее не ощущалось, что изменяет физическую картину происходящих явлений и приводит к качественному скачку процесса накопления повреждений. При катастрофическом износе изменения состояния объекта, как и при приработке, взаимно зависимы и носят направленный характер.

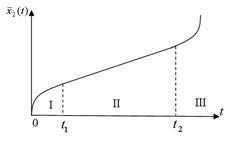
Рис. 2.3. Типичная кривая износа

Из рис 2.3 с учётом (2.26) и рис.2.2 следует, что среднее число накопленных повреждений за время t на этапе 2 составит:

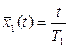, (2.28)

а соответствующая этому числу средняя величина износа за время t составит:

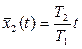. (2.29)

На основе (2.28), (2.29) и обозначений (2.27) математическое ожидание величины износа, а также его скорость соответственно составят

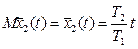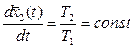; . (2.30)

В формулах (2.30) отношение 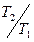есть средняя скорость износа. Так как это отношение от времени не зависит, то средняя скорость износа на этапе II является величиной постоянной.

Даная модель процесса износа (2.30) отвечает ситуации, когда приработка закончена, а катастрофический износ ещё не наступил. Скорость износа в этом случае (см. рис.2.3.) постоянна.

Из формул (2.23), (5,24), (5,25) вытекает, что с учётом ранее ввёденных обозначений (2.27) интервалы 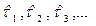между одиночными повреждениями подчинены одному и тому же экспоненциальному закону распределения с параметром 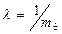. Действительно, поскольку из рис. 2.3. и формул (2.28)-(2.30) на нормальном этапе эксплуатации имеет место:

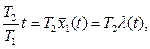(2.31)

где 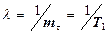- величина обратная среднему времени между включениями объекта.

Отсюда следует важное положение, заключающееся в том, что случайная длительность 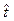процесса накопления повреждений до отказа определяется суммой интервалов времени подчинённых экспоненциальному закону распределения с параметром, определяемым формулой (2.25), то есть:

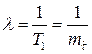. (2.32)

В этом случае данной схеме накапливающихся повреждений отвечает гамма-распределение случайной величины 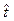с плотностью [2-6, 15-21]

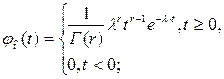(2.33)

где r - число повреждений, необходимых для возникновения отказа, Г(r) – гамма-функция, которая в общем случае определяется формулой [2-5,20,21]

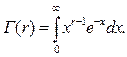(2.34)

Однако число повреждений r является целочисленной величиной, для которой справедливо соотношение [2-5]

Г(r) = (r-1)!. (2.35)

В общем случае функция распределения случайной величины 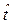то есть времени достижения износом с учётом плотности (2.34) предельного значения подчинена закону Эрланга, определяемого формулой [4-6]

, (2.36)

где t - заданное время функционирования объекта.

Для целых r после интегрирования по частям формула (2.36) принимает вид:

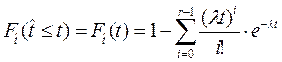. (2.37)

Формула (2.37) дает распределение времени 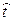, при котором достигается число повреждений, равное r.

При r=1 плотность (2.33) совпадает с плотностью экспоненциального распределения, описывающего модель возникновения внезапного отказа (2.23)-(2.25).

Кривые плотности случайной величины 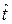, подчинённой закону Эрланга для различных значений r=1,5,…,15 при 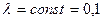, приведены на рис. 2.4.

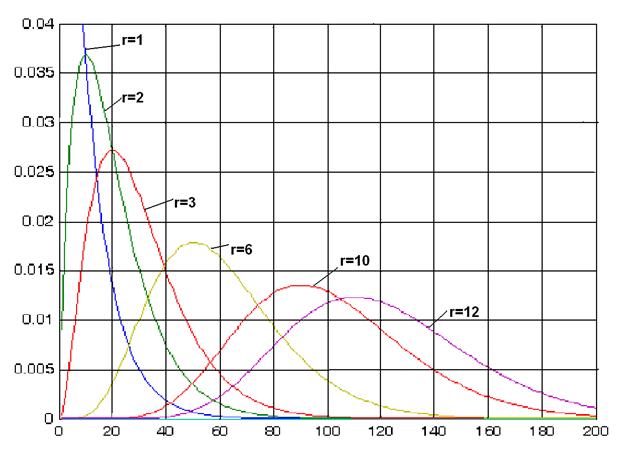
Рис. 2.4. Плотность гамма-распределения при разных r и .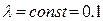

При малых r кривые плотности гамма-распределения (2.37) ассиметричны, с ростом r они становятся все более симметричными (см. рис.2.4).

Математическое ожидание 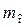и дисперсия 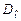гамма-распределения имеют вид [2-6]:

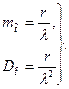(2.38)

Формально считается, что переход к нормальному распределению приемлем, если имеет место соотношение [2-5,10]:

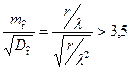, (2.39)

что достигается при r>10…12.

В основе этого предположения лежит то обстоятельство, что с ростом числа r кривая плотности 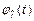гамма-распределения, задаваемого выражением (2.33), стремится к виду приведено на рис. 2.4:

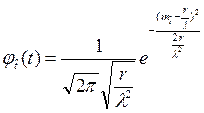, (2.40)

поскольку в соответствие с теоремой Ляпунова распределение суммы большого числа независимых, одинаково распределенных случайных величин, близко к нормальному [2-5,16,18,22].

В общем случае формула (2.40) с учетом (2.58) может быть представлена в виде:

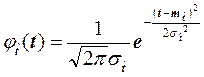. (2.41)

Тогда функция распределения случайной величины 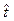, подчиненной нормальному закону распределения с плотностью (2.41) запишется в нормированной форме следующим образом [2,5,7]:

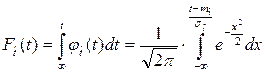, (2.42)

где - функция Лапласа, представляемая в табулированном виде [2,6,7].

С учётом табулированной функции Лапласа функция распределения случайной величины 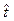принимает вид [2-5]:

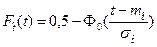, (2.43)

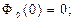
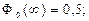
где 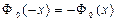[2-9].

Выражение (2.43) с хорошей для практики точностью аппроксимируется логистической зависимостью вида:

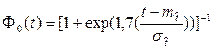, (2.44)

что значительно облегчает вычисления и позволяет моделировать значения случайных величин методом обратной функции [2-5,18].

Интенсивность (опасность) отказа l(t) в случае нормального распределения монотонно возрастает, приближаясь к асимптоте 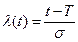. Монотонное возрастание l(t) — характерный признак нормального распределения. График функции l(t) показан на рис 2.5.

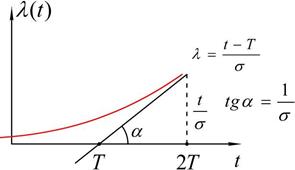
Рис. 2.5. График функции l(t).

Как известно, при экспоненциальном распределении интенсивность отказов постоянна (2.32), поэтому любое профилактическое обслуживание (ремонт и. т. д.) не может повысить надёжность объекта. Это обстоятельство обусловило рассмотрение ряда других законов, среди которых важную роль играет двухпараметрическое распределение Вейбулла. Впервые это распределение было выдвинуто Вейбуллом в 1939 году для описания усталостной прочности материалов.

Вероятность безотказной объекта, подчиняющегося закону Вейбулла, имеет вид [2-6]:

.

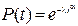Варьируя в этом распределении параметрами α и λ можно добиться хорошего совпадения статистических данных с теоретической моделью, которые не удаётся аппроксимировать однопараметрическим показательным законом. Из этого распределения вытекает ряд частных случаев: экспоненциальное при α=1, Релея при α=2, приближенно-нормальное при .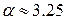

Такая универсальность закона Вейбулла позволяет использовать один и тот же математический аппарат при исследовании самых различных объектов. Закон Вейбулла имеет под собой определённо физические предпосылки. Так, закон Вейбулла описывает надёжность нерезервированного объекта состоящего из большого числа элементов с примерно одинаковыми характеристиками надёжности. Среднее время безотказной работы объекта, подчиняющегося закону Вейбулла имеет вид [5,15,18]

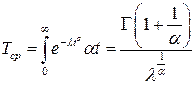
где 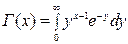- гамма функция

Интенсивность отказf, определяемая как [2-5]

,

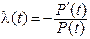имеет вид .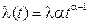

При α<1 интенсивность отказов убывает, а при α>1 возрастает. Варьируя параметром α распределения Вейбулла, его можно использовать для описания как «молодеющих» так и «стареющих» объектов. Гироскопические элементы и устройства хорошо описываются этим законом.

Плотность распределения Вейбулла 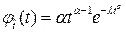имеет вид (см. рис.2.6.):

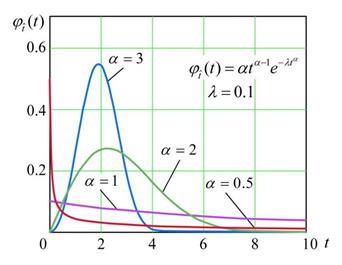
Рис.2.6. Плотность вероятности распределения безотказной работы объекта, подчиненного закону Вейбулла.

Действительно, распределению Вейбулла подчинена наработка до отказа объекта, состоящего из 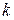параллельно соединенных элементов, безотказность каждого из них подчинена экспоненциальному закону распределения

.

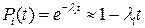Тогда вероятность безотказной работы данного объекта составит

,

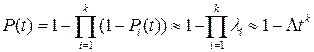где 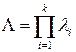- интенсивность отказа объекта, состоящего из 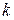параллельно соединенных однотипных элементов.

При 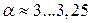распределение Вейбулла практически совпадает с нормальным распределением (рис. 2.6).