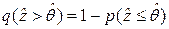Модель “Нагрузка – сопротивляемость объекта”.
Рассмотренные в п.п. 2.1, 2.2 модели основываются на том, что используемые для их построения значения показатели безотказности 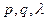 невосстанавливаемых объектов известны.
невосстанавливаемых объектов известны.
Однако получение, значений этих показателей ввиду высокой стоимости и малосерийности сложных современных объектов, в частности объектов РКТ, известными статистическими методами весьма затруднительно.
Эти трудности можно обойти, если использовать дополнительную информацию о законах распределения сопротивляемости (прочности, несущей способности) объекта и нагрузки, воздействующей на объект. При этом считается, что отказ наступит, когда нагрузка, воздействующая на объект, превысит предельное значение соответствующего свойства объекта, то есть его сопротивляемость этой нагрузке [8,9,16,18].
В общем случае нагрузка 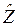 и соответствующая ей сопротивляемость
и соответствующая ей сопротивляемость 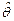 объекта вследствие многообразия и случайной природы факторов, нагружающих объект, а также обуславливающих его прочность при проектировании и изготовлении, являются случайными величинами.
объекта вследствие многообразия и случайной природы факторов, нагружающих объект, а также обуславливающих его прочность при проектировании и изготовлении, являются случайными величинами.
Тогда с учётом (2.1), (2.2) критериями безотказной работы объекта при единичном цикле нагружения могут служить дважды неопрёделенные предикаты вида [14-16]:
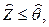 (2.45)
(2.45)
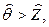 (2.46)
(2.46)
а критериями отказа – предикаты:
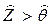 , (2.47)
, (2.47)
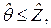 (2.48)
(2.48)
где ^ - символ случайной величины.
Закон распределения случайной величины 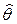 известен или может быть получен по результатам заводских испытаний, а закон распределения случайной величины
известен или может быть получен по результатам заводских испытаний, а закон распределения случайной величины 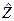 может быть получен по результатам телеметрического контроля или специальных измерений в процессе испытаний и эксплуатации как самого объекта, так и объектов-аналогов.
может быть получен по результатам телеметрического контроля или специальных измерений в процессе испытаний и эксплуатации как самого объекта, так и объектов-аналогов.
Допустимые значения случайных величин 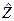 и
и 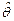 обычно оговариваются в нормативно-технической (НТД), конструкторской и эксплуатационной документации (КД и ЭД).
обычно оговариваются в нормативно-технической (НТД), конструкторской и эксплуатационной документации (КД и ЭД).
Таким образом, при известных плотностях распределения 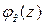 ,
, 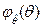 случайных величин
случайных величин 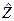 и
и 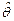 вероятности выполнения предикатов (2.45), (2.46), то есть показатели безотказности объекта при единичном нагружении, могут быть определены следующим образом [2-9,18]:
вероятности выполнения предикатов (2.45), (2.46), то есть показатели безотказности объекта при единичном нагружении, могут быть определены следующим образом [2-9,18]:
|
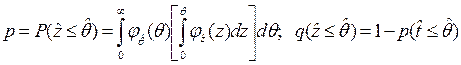 ; (2.49)
; (2.49)
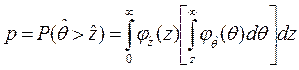 . (2.50)
. (2.50)
В общем случае объект и его элементы подвергаются ряду последовательных нагружений. При этом, если нагрузка, действующая на объект, в вероятностном смысле остаётся постоянной, то вероятность безотказного функционирования объекта при n циклах нагружения на основе формулы (2.49) может быть представлена следующим образом:
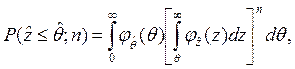 (2.51)
(2.51)
где 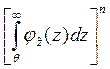 - вероятность того, что за n последовательных циклов нагружения нагрузка ни разу не превзойдёт сопротивляемость объекта или вероятность того, что n независимых циклов нагружения дадут значения
- вероятность того, что за n последовательных циклов нагружения нагрузка ни разу не превзойдёт сопротивляемость объекта или вероятность того, что n независимых циклов нагружения дадут значения 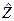 , не превышающие величину сопротивляемости объекта при каждом цикле нагружения.
, не превышающие величину сопротивляемости объекта при каждом цикле нагружения.
В качестве нагрузки и сопротивляемости принимаются одни и те же физические параметры, например, если z – рабочее давление, то θ - давление разрушения, если z – сжимающее усилие, то θ - критическая сила потери устойчивости, если z – рабочая температура, то θ - предельная термостойкость, если z электрическое напряжение, то θ – предельно допустимое значение напряжения и т.д.
Вместе с тем выбор той или иной пары параметров в качестве z и θ достаточно произволен и определяется особенностями конструкции объекта и его назначением.
Полученные на основе выражений (2.49), (2.50) вероятности отказа объекта при единичном цикле нагружения представлены в таблице 2.1 с учётом следующих обозначений:
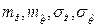 - математические ожидания и среднеквадратические отклонения CB
- математические ожидания и среднеквадратические отклонения CB 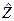 и
и 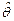 ;
;
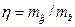 - коэффициент безопасности, представляющий собой отношение математических ожиданий случайных величин
- коэффициент безопасности, представляющий собой отношение математических ожиданий случайных величин 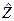 и
и 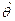 ;
;
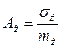 ;
; 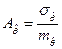 - коэффициенты вариации CB
- коэффициенты вариации CB 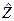 и
и 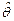 .
.
Расчёты показывают, что для малых значений вероятностей 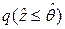 (2.49), соответствующих уровню современных требований к надёжности или безопасности, значения
(2.49), соответствующих уровню современных требований к надёжности или безопасности, значения 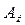 ,
, 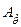 практически не зависят от вида законов распределения случайных величин
практически не зависят от вида законов распределения случайных величин 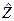 и
и 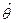 . При этом значения
. При этом значения 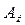 ,
, 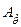 рекомендуется задавать в пределах [5,8,9]:
рекомендуется задавать в пределах [5,8,9]:
(0.1…0.30). (2.52)
Значения 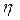 на основе соответствующих требований нормативно-технической и конструкторской документации рекомендуется задавать в пределах [16]
на основе соответствующих требований нормативно-технической и конструкторской документации рекомендуется задавать в пределах [16]
(1.2….2.0). (2.53)
Показатель типа 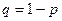 , полученный из (2.49), (2.50) для широкого класса двухпараметрических распределений, является сложной функцией вида
, полученный из (2.49), (2.50) для широкого класса двухпараметрических распределений, является сложной функцией вида
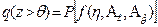 , (2.54)
, (2.54)
где 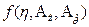 - функция трёх аргументов
- функция трёх аргументов 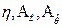 , являющаяся в свою очередь аргументом функции Р.
, являющаяся в свою очередь аргументом функции Р.
Формулы таблицы 2.1 позволяют численно рассчитать значения показателей (2.49), (2.50) надежности.
Таблица 2.1
| № | Вид законов распределения | Плотность вероятности | Плотность вероятности | Вероятность | |
| п/п | 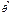
| 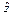
| 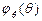
| 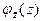
| q=1-p |
| Нормальный | Нормальный | 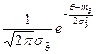
| 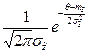
| 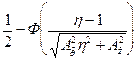
| |
| Экспоненциальный | Экспоненциальный | 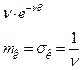
| 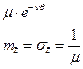
|
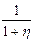
| |
| Нормальный | Экспоненциальный | 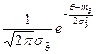
| 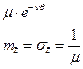
| 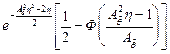
| |
| Экспоненциальный | Нормальный | 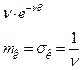
| 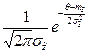
| 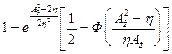
| |
| Релея | Релея | 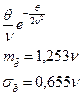
| 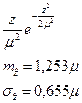
|
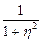
|
Дата добавления: 2016-09-26; просмотров: 1811;