Поле плоского конденсатора

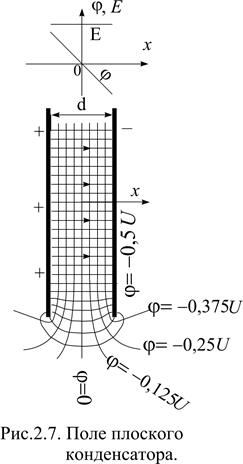Плоским конденсатором называется электродная система из двух параллельных пластин, называемых обкладками конденсатора. Расстояние между обкладками обычно значительно меньше их длины и ширины. При таких условиях почти все заряды оказываются практически равномерно распределенными по внутренним поверхностям обкладок. В пространстве между обкладками вдали от краев поле однородно, т.е. вектор напряженности поля Е постоянен и направлен по нормали к поверхности обкладок. Силовые линии поля представляют собой прямые линии, параллельные нормали. Для описания такой электродной системы применим декартову систему координат с осью х, параллельной нормали к поверхности, и началом координат, расположенным в центре конденсатора на середине расстояния между пластинами. Используя определение электрического смещения (1.22)-(1.23), можно записать:

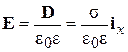, (2.23)

где s=Q/S – поверхностная плотность заряда на обкладках, которая является постоянной величиной вдали от краев обкладок. К задаче подходят фундаментальные решения уравнения Лапласа (2.1). Сравнивая выражения (2.1) и (2.23) определяем постоянную интегрирования С₁:

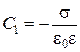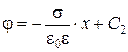и (2.24)

Пусть потенциал j = 0 по центру между обкладками конденсатора при х = 0. Тогда С₂ = 0. Напряжение между обкладками конденсатора равно:

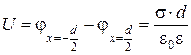, откуда 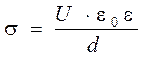и 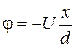(2.25)

Эквипотенциальные поверхности представляют собой плоскости, параллельные обкладкам (x = const). При графическом изображении поля плоского конденсатора расстояние между эквипотенциальными поверхностями должно быть одинаково для того, чтобы потенциалы отличались на одну и ту же величину. Заряд конденсатора Q = s×S, где S- площадь обкладки. Емкость конденсатора равна

C = Q/U = 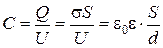(2.26)

Поле плоского конденсатора является равномерным только вдали от краев. При приближении к краю линии поля искривляются, и расчет параметров поля (напряженности, потенциала) следует проводить по более сложным формулам, чем (2.23)-(2.26). Эти формулы будут получены при рассмотрении метода конформных отображений.